Một số mô hình có sự xuất hiện của biến mẹ chứa các biến con, biến dạng này gọi là biến bậc hai và các biến con bên trong gọi là biến bậc một thành phần. Bài viết này sẽ hướng dẫn các bạn phân tích nhân tố khẳng định CFA với mô hình có biến bậc hai, bao gồm khái niệm, cách biểu diễn trên diagram và phân tích, đọc kết quả.
1. Biến bậc hai (second-order) và biến bậc một (first-order)
Trong thuật ngữ thống kê chúng ta gọi là biến bậc hai – biến bậc một. Còn trong trao đổi, nói chuyện chúng ta có thể sử thêm cụm biến mẹ – biến con hoặc biến mẹ – biến thành phần để hiểu một cách trực quan hơn đó là một biến mẹ sẽ chứa các biến con bên trong.
Xét cấu trúc biến bậc hai như sau: Biến bậc hai MKT (Marketing) gồm 4 thành phần biến bậc một là PP (Phân phối), GC (Phân phối), SP (Sản phẩm), KM (Khuyến mãi). Khi biểu diễn trên mô hình lý thuyết, có thể vẽ dạng như sau:
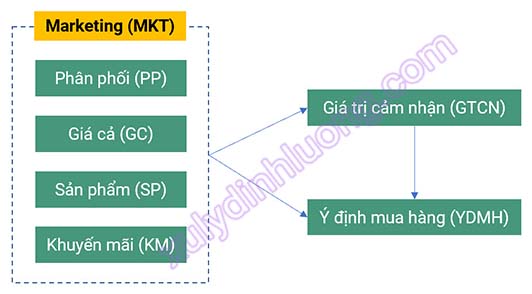
Thông tin biến:
– MKT: Biến bậc 2, không có biến quan sát. Lưu ý rằng, biến bậc 2 được đo lường thông qua các biến bậc 1, do đó biến bậc 2 không có biến quan sát.
– PP: Biến bậc 1, gồm 2 biến quan sát, là biến thành phần của biến MKT.
– GC: Biến bậc 1, gồm 4 biến quan sát, là biến thành phần của biến MKT.
– SP: Biến bậc 1, gồm 4 biến quan sát, là biến thành phần của biến MKT.
– KM: Biến bậc 1, gồm 2 biến quan sát, là biến thành phần của biến MKT.
– GTCN: Biến bậc 1, gồm 3 biến quan sát.
– YDMH: Biến bậc 1, gồm 4 biến quan sát.
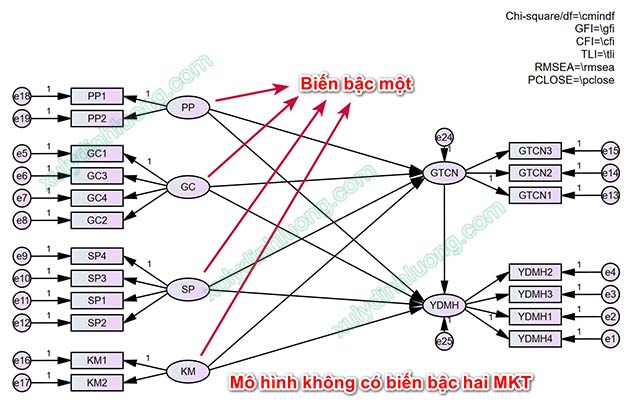
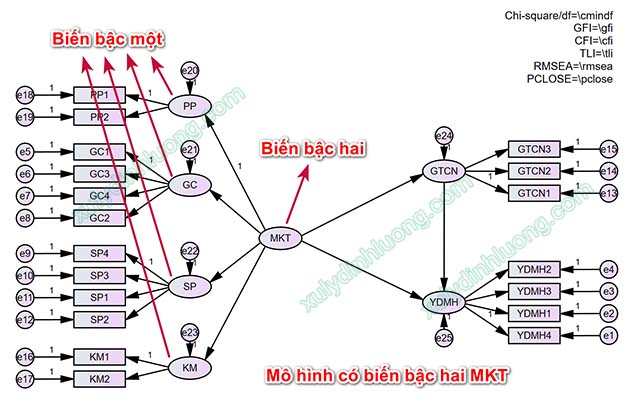
Đặc điểm của biến bậc hai:
– Không có biến quan sát đo lường trực tiếp
– Được đo lường thông qua các biến bậc một thành phần
– Khi biểu diễn trên phần mềm SEM, nó là biến tiềm ẩn và được vẽ bằng hình tròn hoặc elip.
– Nếu có biến bậc hai chỉ đánh giá được mối quan hệ biến bậc hai lên các biến khác, không thể cùng lúc đánh giá biến bậc hai và biến bậc một thành phần lên các biến khác.
– Nếu muốn đánh giá cả mối quan hệ biến bậc hai và biến thành phần bậc một lên các biến khác, sẽ vẽ 2 diagram và đánh giá riêng ở mỗi diagram.
2. Xử lý CFA biến bậc hai trên AMOS
Theo Zainudin, A. (2012). A handbook on SEM: Structural equation model- ling using amos graphics (2th ed.). Kelantan: University Technology MARA Press, để xử lý biến bậc hai trong CFA, chúng ta sẽ đánh giá:
#1: Tính hội tụ các biến bậc một
#2: Ý nghĩa của các biến bậc một trong biến bậc hai
#3: Đánh giá mô hình tổng thể của nghiên cứu. Các tiêu chí đánh giá gồm: độ phù hợp tổng thể mô hình; chất lượng biến quan sát; tính hội tụ, tính phân biệt của biến bậc hai với các biến khác trong mô hình tổng thể.
2.1 Đánh giá tính hội tụ các biến bậc một
Để đánh giá tính hội tụ các biến bậc một, chúng ta vẽ diagram chỉ biểu diễn mối quan hệ giữa các biến bậc một thuộc một biến bậc hai với nhau.
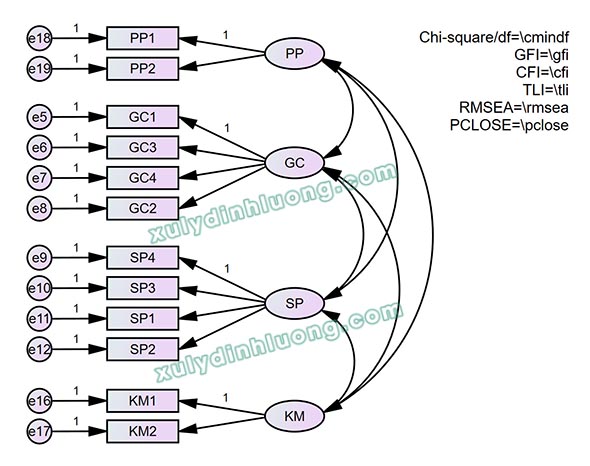
Sử dụng plugin Validity and Reliability Test để đánh giá tính hội tụ, tính phân biệt theo hướng dẫn tại bài viết Đánh giá tính hội tụ, tính phân biệt trong phân tích CFA.
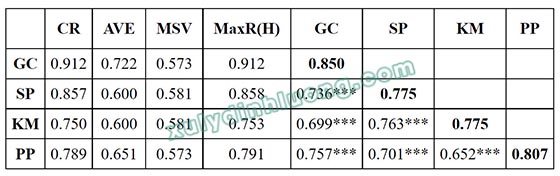
→ Giá trị CR đều lớn hơn 0.7 và AVE đều lớn hơn 0.5, như vậy các thang đom biến bậc một đều đảm bảo tính hội tụ.
2.2 Ý nghĩa của các biến bậc một trong biến bậc hai
Để đánh giá ý nghĩa của các biến bậc một trong biến bậc hai, chúng ta vẽ diagram biểu diễn mối quan hệ giữa biến bậc hai với biến bậc một thành phần như bên dưới.
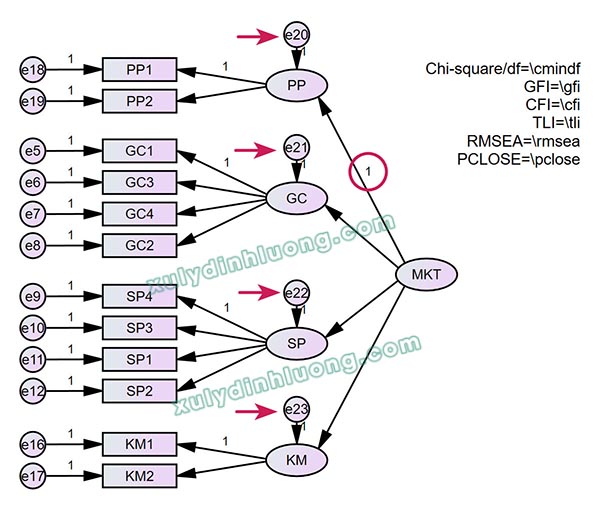
Những chú ý khi biểu diễn biến bậc hai trên CFA AMOS:
1. Trong các mũi tên đường dẫn từ biến bậc 2 sang biến bậc 1 thành phần, phải gán hệ số chặn 1 ở mục Regression weight cho một trong các mũi tên đường dẫn này.
2. Mỗi biến bậc một thành phần phải có phần dư (sai số), cụ thể trong ảnh ở trên 4 phần dư có tên tương ứng là e20 đến e23.
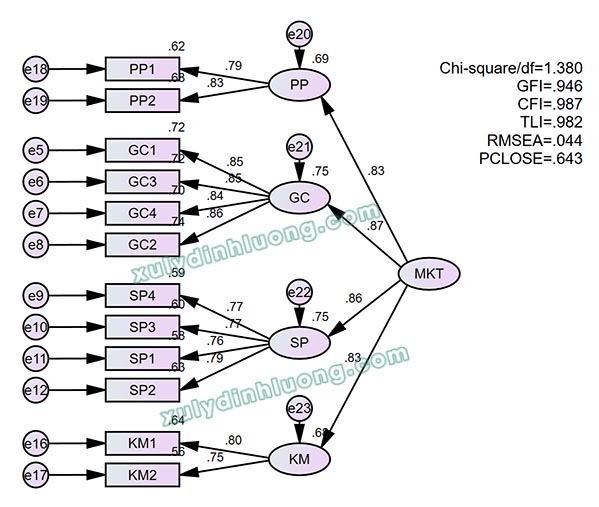
Từ output kết quả, chúng ta vào Estimates > Scalars > Regression Weights.
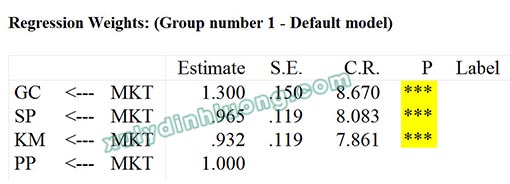
→ Giá trị P-value các mối tác động từ biến bậc hai lên biến bậc một thành phần đều nhỏ hơn 0.05. Như vậy, các biến bậc một đều có ý nghĩa giải thích cho biến bậc hai. Với biến PP là biến có hệ số tải 1.000 là giá trị tham chiếu nên sẽ không có chỉ số.
Tiếp tục vào Estimates > Scalars > Standardized Regression Weights.
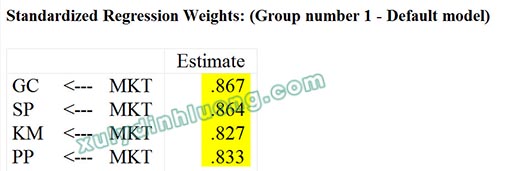
→ Giá trị hệ số tải (factor loading – trong amos lúc này là standardized regression weights) của các biến bậc một thành phần cao đáng kể so với mức 0.5 (Hair và cộng sự (2009). Như vậy, các biến bậc một đều đóng góp vào biến bậc hai rất tốt. Hệ số tải nào lớn hơn sẽ cho thấy biến bậc một đó đóng góp nhiều hơn vào biến bậc hai.
2.3 Đánh giá CFA mô hình tổng thể của nghiên cứu
Trong diagram này, chúng ta sẽ đánh giá độ phù hợp mô hình tổng thể của biến bậc hai. Xét diagram quan hệ biến bậc hai với các biến khác trong mô hình.
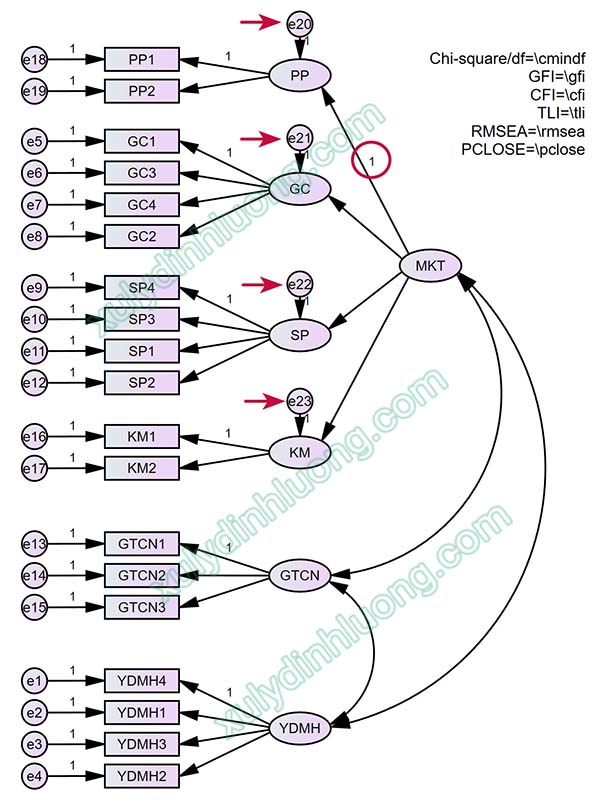
Thêm một chú ý khi biểu diễn biến bậc hai trên CFA AMOS với mô hình tổng thể:
Mũi tên hai chiều biểu diễn covariance giữa các biến tiềm ẩn sẽ được nối từ biến bậc hai tới các biến tiềm ẩn khác, không nối từ các biến bậc một thành phần. Cụ thể trong ảnh ở trên, có 3 mũi tên hai chiều được nối giữa các biến MKT, GTCN, YDMH, không nối ở các biến PP, GC, SP, KM.
a. Đánh giá độ phù hợp tổng thể
Đánh giá độ phù hợp tổng thể mô hình qua các chỉ số model fit, chi tiết các đánh giá bạn xem tại bài viết Kiểm định độ phù hợp mô hình Model Fit trong CFA.
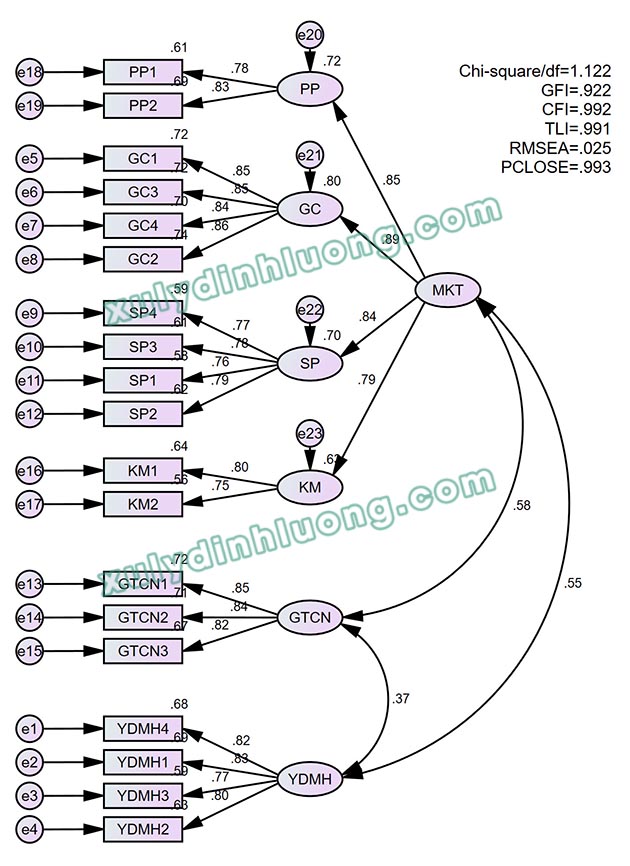
→ Các chỉ số độ phù hợp mô hình đều vượt ngưỡng chấp nhận:
GFI = 0.922 > 0.9
CFI = 0.992 > 0.9
TLI = 0.991 > 0.9
RMSEA = 0.025 < 0.08
PCLOSE = 0.993 > 0.05
Như vậy mô hình đạt được độ phù hợp tốt.
b. Chất lượng biến quan sát
Để đánh giá chất lượng biến quan sát trong CFA, chúng ta dựa vào hai bảng kết quả là Regression Weights và Standardized Regression Weights. Từ giao diện bên trái của output, nhấp vào Regression Weights.
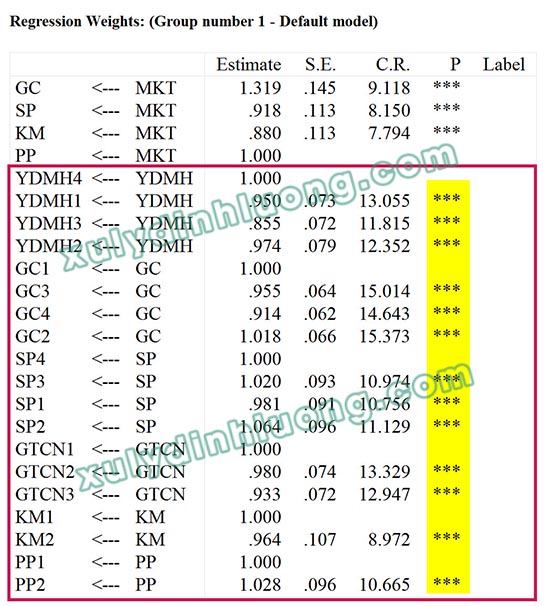
→ Giá trị P-value các biến quan sát đều nhỏ hơn 0.05. Như vậy, các biến quan sát đều có ý nghĩa trong mô hình.
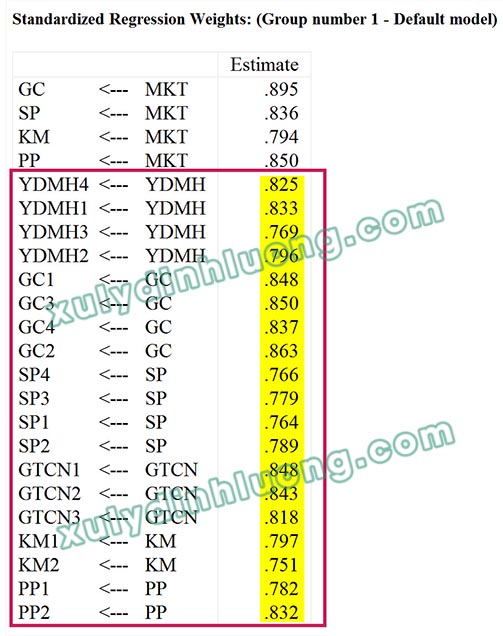
→ Hệ số tải nhân tố factor loading (standardized regression weights) của các biến quan sát đều lớn hơn 0.5 (Hair và cộng sự, 2009). Như vậy các biến quan sát đều có ý nghĩa trong mô hình.
c. Tính hội tụ, tính phân biệt các biến trong mô hình tổng thể
Sử dụng plugin Validity and Reliability Test để đánh giá tính hội tụ, tính phân biệt theo hướng dẫn tại bài viết Đánh giá tính hội tụ, tính phân biệt trong phân tích CFA.
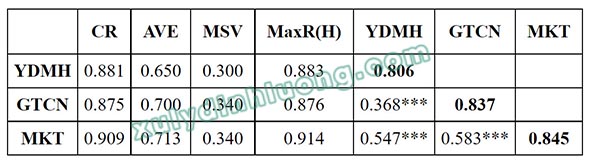
→ Giá trị CR đều lớn hơn 0.7 và AVE đều lớn hơn 0.5, như vậy các thang đom biến bậc một đều đảm bảo tính hội tụ (Hair và cộng sự, 2009).
→ Căn bậc hai của AVE (các số bôi đậm) lớn hơn các tương quan giữa các biến tiềm ẩn với nhau (hệ số tương quan nằm ở phần dưới đường chéo in đậm) , giá trị MSV nhỏ hơn AVE, do vậy tính phân biệt được đảm bảo (Fornell & Larcker, 1981).
Xem tiếp: Phân tích SEM mô hình có biến bậc hai second-order AMOS












