Phân tích nhân tố khám phá EFA mô hình biến bậc hai có nhiều khác biệt so với mô hình chỉ thuần về biến bậc một. Bài viết này chúng ta sẽ đi chi tiết vào hai dạng mô hình biến bậc hai tương ứng hai phương thức kỳ vọng kết quả EFA đạt được khác nhau.
Trước khi đi vào nội dung chính của bài viết, chúng ta ôn lại kiến thức về tính hội tụ và phân biệt của các nhân tố được thể hiện trong kết quả ma trận xoay EFA:
- Hội tụ: Các biến quan sát cùng tính chất, cùng thể hiện chung một đặc điểm sẽ được gom chung lại với nhau về một cột. Việc hội tụ về chung thành một nhân tố, nếu xét về mặt dữ liệu là do các biến này có sự tương quan mạnh với nhau.
- Phân biệt: Từng nhóm biến tách nhau ra thành từng cột riêng biệt. Việc phân biệt nhau thành từng nhân tố, nếu xét về mặt dữ liệu là do các biến trong nhân tố này có tương quan thấp với các biến trong nhân tố khác.
1. Quan hệ biến bậc hai và bậc một là Reflective
Nếu mối quan hệ bậc hai – bậc một là mô hình kết quả reflective. Các biến bậc một là kết quả được tạo ra từ biến bậc hai (mũi tên hướng từ biến bậc hai sang bậc một) nên giữa chúng sẽ tồn tại sự tương quan tương đối mạnh. Giả sử ví dụ ở dưới, quan hệ từ biến MKT lên bốn biến PP, GC, SP, KM là reflective.
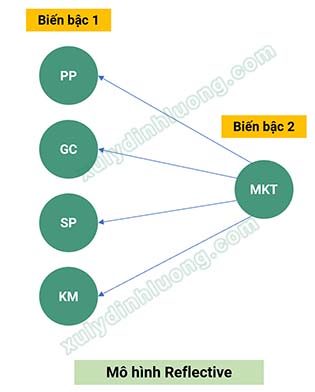
Các biến bậc một tương quan mạnh với nhau, dẫn đến các biến quan sát con của chúng cũng tương quan mạnh với nhau. Như đề cập ở phần mở đầu, khi các biến quan sát tham gia vào EFA mà giữa chúng có sự tương quan mạnh với nhau, sẽ được hội tụ về thành một nhân tố. Dựa trên tính chất này, kỳ vọng khi phân tích EFA đó là các biến quan sát của PP, GC, SP, KM nằm cùng một cột với nhau trong ma trận xoay.
Trong trường hợp giữa các biến bậc một có một, một vài hoặc tất cả biến tách riêng thành một cột so với các nhóm khác, điều này cũng là bình thường. Tình huống này xảy ra khi các biến bậc một thành phần có sự tương quan không quá mạnh. Chúng ta vẫn sử dụng kết quả đó và thực hiện phân tích CFA bình thường, việc đánh giá biến bậc một đó có ý nghĩa hay không sẽ dựa vào độ tin cậy (chỉ số CR) và tính hội tụ (chỉ số AVE, hệ số Standardized Loading Estimates các biến bậc một) của biến MKT trong phân tích CFA.
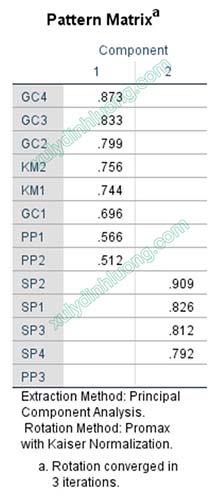
Nếu kết quả EFA cho chạy chung tất cả các biến trong mô hình mang lại kết quả tốt chúng ta nên chạy chung. Trường hợp xuất hiện sự xáo trộn nhiều, ma trận xoay lộn xộn, nên tách chạy EFA cho biến bậc hai riêng, và các biến còn lại trong mô hình riêng.
2. Quan hệ biến bậc 2 và bậc 1 là Formative
Nếu mối quan hệ bậc hai – bậc một là mô hình nguyên nhân formative. Các biến bậc một là nguyên nhân tạo ra biến bậc hai hay nói cách khác, các biến bậc một là một thành phần cấu tạo nên biến bậc hai (mũi tên hướng từ biến bậc một sang bậc hai). Lúc này, các biến bậc một mỗi biến là một thành phần riêng biệt nên giữa chúng thường có tương quan yếu. Giả sử ví dụ ở dưới, quan hệ từ biến MKT lên bốn biến PP, GC, SP, KM là formative.
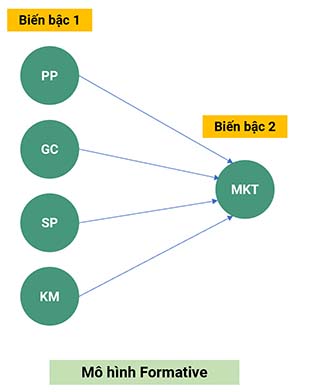
Các biến bậc một tương quan yếu với nhau, dẫn đến các biến quan sát con của chúng cũng tương quan yếu với nhau. Như đề cập ở phần mở đầu, khi các biến quan sát tham gia vào EFA mà giữa chúng có sự tương quan thấp với nhau, sẽ được tách thành từng cột riêng biệt. Dựa trên tính chất này, kỳ vọng khi phân tích EFA đó là các biến quan sát của PP, GC, SP, KM sẽ nằm ở mỗi cột tách biệt với nhau trong ma trận xoay.
Sự kỳ vọng EFA của biến bậc một formative tương tự với kỳ vọng EFA giữa các biến độc lập. Mỗi biến bậc một lúc này hoàn toàn giống như là một biến độc lập.
Trong trường hợp giữa các biến bậc một có sự gộp nhóm, tách nhóm khác với lý thuyết như hai nhóm biến bậc một hội tụ về một cột hoặc một nhóm biến bị tách thành hai nhóm nhỏ… Chúng ta sẽ hiệu chỉnh lại mô hình biến bậc một thành phần, đặt tên các biến bậc một mới và xử lý bình thường.
Tình huống gộp/tách biến bậc một so với cấu trúc lý thuyết hoàn toàn giống như gộp/tách biến độc lập. Do đó, chúng ta xử lý EFA ở các biến độc lập thế nào sẽ xử lý biến bậc một formative như vậy.
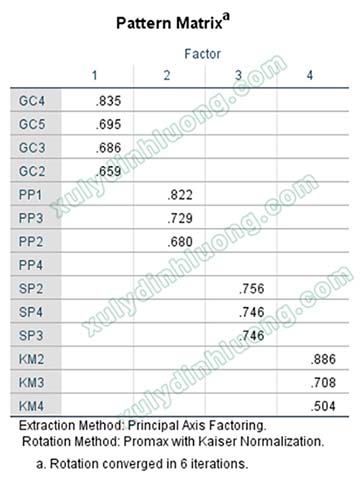
Nếu kết quả EFA cho chạy chung tất cả các biến trong mô hình mang lại kết quả tốt chúng ta nên chạy chung. Trường hợp xuất hiện sự xáo trộn nhiều, ma trận xoay lộn xộn, nên tách chạy EFA cho biến bậc hai riêng, và các biến còn lại trong mô hình riêng.












