Đánh giá hiện tượng cộng tuyến trong mô hình SEM trên AMOS

Trong quá trình phân tích SEM, các chỉ số như VIF, Tolerance là những công cụ hữu ích để đánh giá mức độ đa cộng tuyến giữa các biến độc lập. Tuy nhiên, AMOS hiện chưa tích hợp đầy đủ các chỉ số này, gây trở ngại cho việc kiểm soát và khắc phục vấn đề đa cộng tuyến trên mô hình SEM, từ đó ảnh hưởng đến độ chính xác của kết quả nghiên cứu.

1. Hệ quả khi xảy ra cộng tuyến trong mô hình SEM

Trong phân tích thống kê, đặc biệt là trong các mô hình hồi quy như SEM, đa cộng tuyến là hiện tượng các biến độc lập có mối tương quan tuyến tính mạnh với nhau. Nói một cách đơn giản, các biến này có xu hướng “đi cùng nhau”, khiến việc xác định ảnh hưởng riêng lẻ của từng biến lên biến phụ thuộc trở nên khó khăn.

– Cộng tuyến (Collinearity): Cộng tuyến xảy ra khi hai biến độc lập có mối tương quan tuyến tính quá mạnh với nhau.

– Đa cộng tuyến (Multicollinearity): Đa cộng tuyến xảy ra khi ba biến độc lập trở lên có tương quan tuyến tính quá mạnh với nhau. Nó là một trường hợp tổng quát hơn của cộng tuyến.

Cho dù là trong mô hình hồi quy tuyến tính hay mô hình cấu trúc tuyến tính SEM phức tạp hơn, hiện tượng đa cộng tuyến đều gây ra những hậu quả nghiêm trọng, ảnh hưởng trực tiếp đến độ tin cậy và khả năng giải thích của mô hình

• Quan hệ tác động có ý nghĩa trở thành không có ý nghĩa, quan hệ không có ý nghĩa lại trở thành có ý nghĩa;
• Đảo ngược dấu tác động của quan hệ âm thành dương, dương thành âm;
• Biến tác động mạnh trở thành biến tác động yếu, biến tác động yếu thành tác động mạnh;
• Hệ số hồi quy chuẩn hóa vượt ngưỡng 1, giá trị R bình phương vượt ngưỡng 1….

Có thể thấy những hệ quả mà cộng tuyến gây ra ở trên, phần đánh giá và kết luận mô hình SEM sẽ hoàn toàn sai lệch.

2. Quy trình 4 bước đánh giá cộng tuyến trong phân tích SEM trên AMOS

Kết quả phân tích SEM cho thấy những dấu hiệu bất thường như hệ số hồi quy chuẩn hóa vượt quá 1, giá trị R bình phương lớn hơn 1 và các mối quan hệ ngược dấu với giả thuyết… Đây là những bằng chứng mạnh mẽ cho thấy sự hiện diện của đa cộng tuyến trong mô hình SEM.

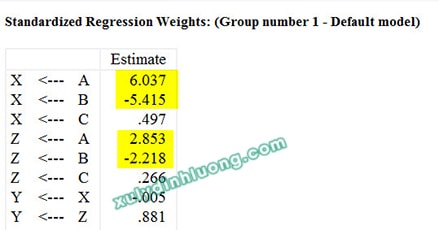
Do AMOS không cung cấp công cụ trực tiếp để đánh giá đa cộng tuyến, chúng ta sẽ tận dụng hồi quy tuyến tính trên SPSS để có được chỉ số VIF đánh giá vấn đề này trong mô hình SEM. Cụ thể, chúng ta sẽ:

Bước 1: Quy đổi mô hình SEM phức tạp thành từng mô hình hồi quy đơn giản

Khi đánh giá đa cộng tuyến trong mô hình SEM, chúng ta cần xem xét từng mối quan hệ giữa các biến độc lập và biến phụ thuộc một cách riêng biệt. Điều này tương đương với việc tách mô hình SEM phức tạp thành các mô hình hồi quy đơn giản con để xác định xem có tồn tại đa cộng tuyến giữa các biến độc lập trong mỗi mô hình con hay không.

Xét mô hình của kết quả phân tích phía trên:

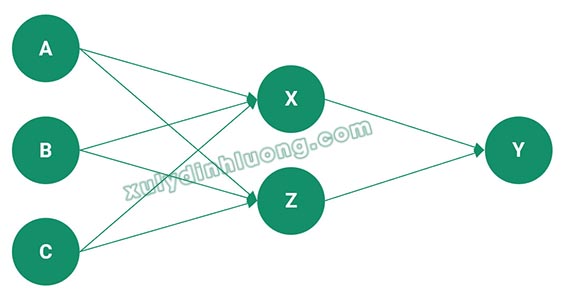
Trong ngữ cảnh của mô hình SEM tổng thể, các biến A, B, và C được gọi là biến độc lập, các biến X và Z là biến trung gian, và biến Y là biến phụ thuộc. Giờ đây, chúng ta sẽ chuyển đổi mô hình phức tạp này thành các mô hình hồi quy đơn giản để dễ dàng phân tích.

Hồi quy là một mô hình trong đó một hoặc nhiều biến độc lập cùng tác động lên một biến phụ thuộc. Do đó, trong mô hình SEM phức tạp, có bao nhiêu biến đóng vai trò phụ thuộc thì sẽ có bấy nhiêu mô hình hồi quy tương ứng. Lưu ý rằng, biến trung gian là loại biến vừa đóng vai trò là biến độc lập, vừa là biến phụ thuộc trong các mối quan hệ khác nhau của mô hình.

Trong mô hình SEM này, các biến X, Z và Y đều đóng vai trò là biến phụ thuộc vì chúng nhận các mũi tên tác động từ các biến khác. Do đó, để đánh giá đa cộng tuyến, chúng ta cần xây dựng 3 mô hình hồi quy đơn giản tương ứng với mỗi biến phụ thuộc này.

– Mô hình hồi quy 1: biến độc lập A, B, C tác động lên biến phụ thuộc X;

– Mô hình hồi quy 2: biến độc lập A, B, C tác động lên biến phụ thuộc Z;

– Mô hình hồi quy 3: biến độc lập X, Z tác động lên biến phụ thuộc Y.

Bước 2: Xác định cách đánh giá hiện tượng cộng tuyến

Từ kết quả phân tích ở bước trước, chúng ta đã xác định được ba mô hình hồi quy đơn giản. Tiếp theo, chúng ta sẽ tập trung vào việc đánh giá đa cộng tuyến trong từng mô hình này. Cụ thể, chúng ta sẽ xem xét mối tương quan giữa các biến độc lập trong mỗi phương trình hồi quy.

– Đánh giá hiện tượng cộng tuyến giữa biến A, B, C (thuộc mô hình 1);

– Đánh giá hiện tượng cộng tuyến giữa biến A, B, C (thuộc mô hình 2);

– Đánh giá hiện tượng cộng tuyến giữa biến X, Z (thuộc mô hình 3).

Bởi vì các biến độc lập trong mô hình hồi quy 1 và 2 giống nhau, nên chúng ta chỉ thực hiện một lần thôi. Như vậy, để đánh giá hiện tượng cộng tuyến của mô hình SEM phức tạp ban đầu chúng ta sẽ cần:

– Đánh giá hiện tượng cộng tuyến giữa biến A, B, C;

– Đánh giá hiện tượng cộng tuyến giữa biến X, Z.

Bước 3: Chuẩn bị dữ liệu các biến để tiến hành phân tích mô hình hồi quy đơn giản

Trong SEM trên AMOS, các biến tiềm ẩn được phần mềm tính toán trực tiếp từ dữ liệu của các biến quan sát trên sơ đồ, nên không cần có dữ liệu riêng cho các biến tiềm ẩn. Ngược lại, khi thực hiện hồi quy trên SPSS, cần tính toán dữ liệu cho các biến tiềm ẩn để đưa vào phần khai báo biến.

Để tạo ra dữ liệu cho các biến tiềm ẩn, chúng ta thường sử dụng hai phương pháp chính: tính tổng hoặc tính trung bình cộng của các biến quan sát cấu thành nên nó. Bạn có thể tham khảo chi tiết hơn về hai phương pháp này trong bài viết này. Khi tính toán dữ liệu biến đại diện bạn nhớ loại bỏ các biến quan sát đã bị loại ở những bước trước SEM như Cronbach Alpha, EFA, CFA…

Khi đặt tên cho các biến đại diện trong dữ liệu SPSS, cần đảm bảo khác biệt với tên của biến tiềm ẩn đã khai báo trong sơ đồ AMOS. Lý do là các biến tiềm ẩn trong AMOS được tính toán trực tiếp từ dữ liệu của biến quan sát mà không cần dữ liệu riêng trong tập dữ liệu đầu vào. Khi tạo biến đại diện trên SPSS, tức là tạo ra dữ liệu cho các biến tiềm ẩn này, có thể dẫn đến xung đột với các tính toán của AMOS. Ví dụ, nếu biến tiềm ẩn trong sơ đồ AMOS được đặt tên là A, B, C, X, Y, và Z, thì trên SPSS có thể thêm tiền tố f_ trước các tên biến đại diện để tránh trùng với tên biến tiềm ẩn trong AMOS.

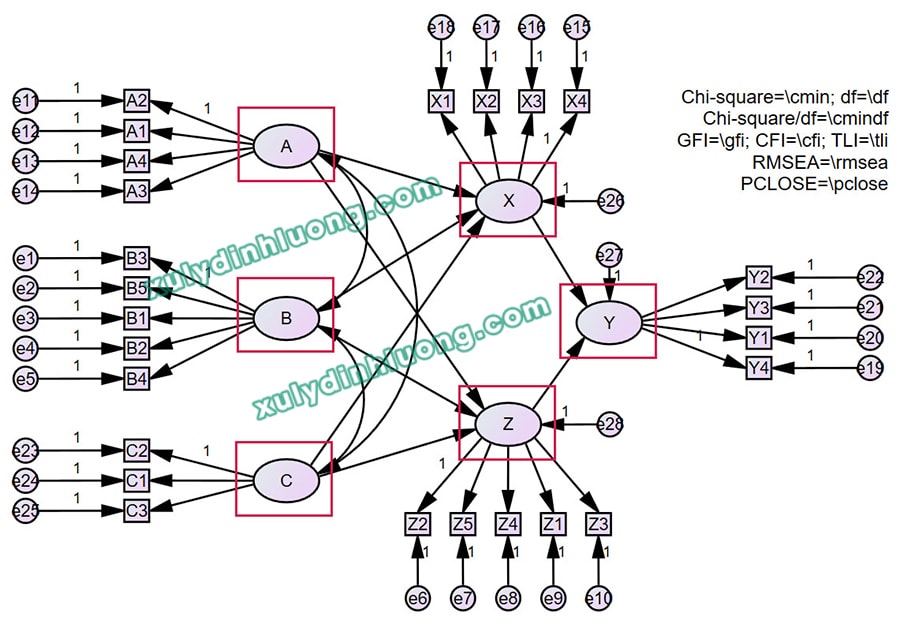
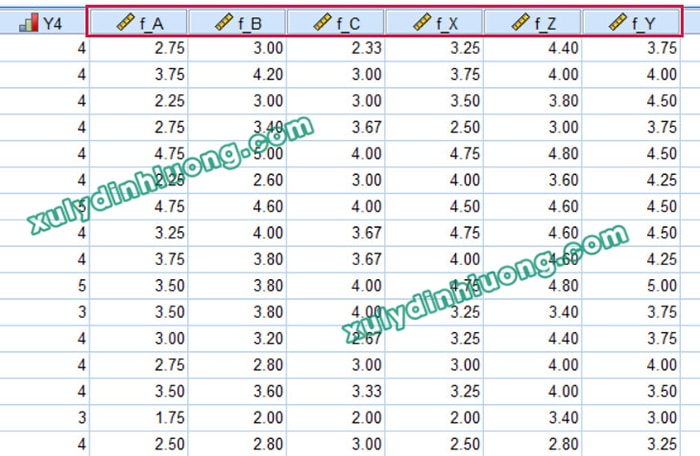
Bước 4: Phân tích hồi quy & đánh giá hiện tượng cộng tuyến dựa trên chỉ số VIF

Ở bước 1, chúng ta đã xác định rằng mô hình SEM bao gồm ba mô hình hồi quy đơn giản. Tiếp theo, chúng ta sẽ thực hiện phân tích ba hồi quy này để thu thập ba bảng kết quả Coefficients, vì bảng này chứa chỉ số VIF, giúp đánh giá hiện tượng cộng tuyến giữa các biến độc lập. Có nhiều ngưỡng VIF được đề xuất trong các nghiên cứu để xác định sự xuất hiện của cộng tuyến, chẳng hạn như VIF > 3, VIF > 3.3, VIF > 5, hoặc VIF > 10. Việc chọn ngưỡng VIF phù hợp sẽ phụ thuộc vào đặc điểm dữ liệu đang phân tích. Nếu kết quả phân tích SEM cho thấy dấu hiệu của cộng tuyến, chúng ta cần xử lý vấn đề này ngay thay vì sử dụng ngưỡng VIF cao như 10 để khẳng định không có cộng tuyến.

– Mô hình hồi quy 1: biến độc lập A, B, C tác động lên biến phụ thuộc X;

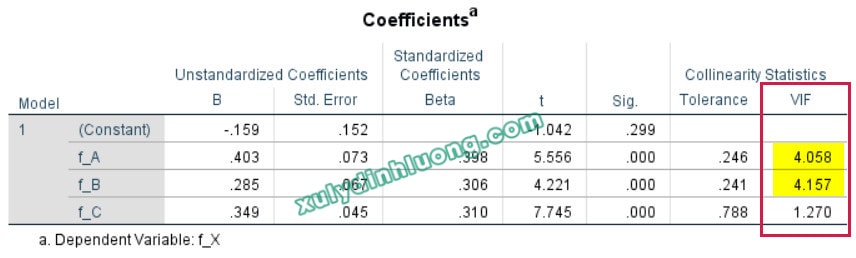
→ Đánh giá hiện tượng cộng tuyến giữa biến A, B, C: biến A và B có VIF lớn hơn 3 (mình sử dụng ngưỡng 3 để nhận diện sự cộng tuyến trong mô hình). Như vậy A-B có cộng tuyến với nhau.

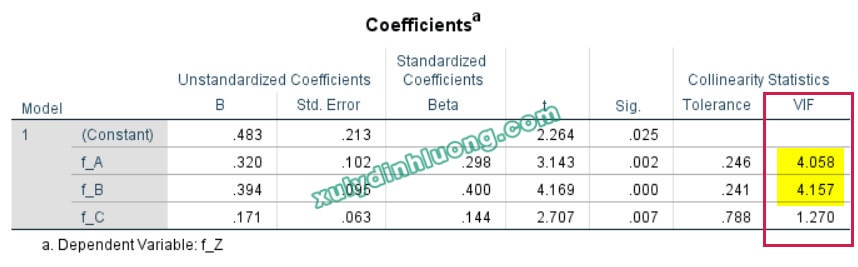
→ Đánh giá hiện tượng cộng tuyến giữa biến A, B, C: có thể thấy giá trị VIF của các biến A, B, C ở bảng thứ hai này hoàn toàn giống với bảng thứ nhất bởi vì VIF là giá trị quan hệ giữa các biến độc lập, bất kể biến phụ thuộc là gì. Do vậy, khi đánh giá vấn đề cộng tuyến chúng ta sử dụng một trong hai bảng là đủ.

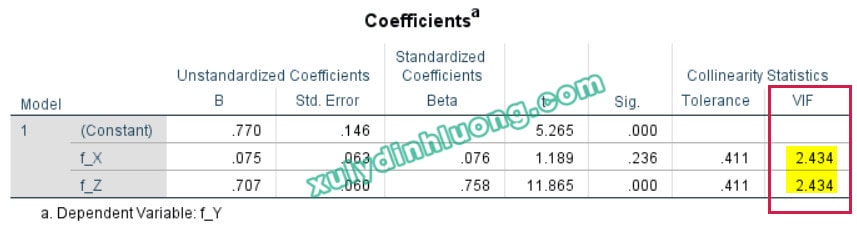
→ Đánh giá hiện tượng cộng tuyến giữa biến X, Z: biến X và Z có VIF nhỏ hơn 3. Như vậy X-Z không có hiện tượng cộng tuyến với nhau. Đối chiếu với kết quả hệ số tác động chuẩn hóa từ X, Z lên Y cũng như là giá trị R2 của Y, các giá trị này đều không vượt quá 1 nên chúng ta càng thêm khẳng định không tồn tại vấn đề cộng tuyến giữa hai biến này.

3. Khắc phục cộng tuyến trong mô hình SEM trên AMOS