Phân tích và đọc kết quả tương quan Pearson trên SPSS

1. Lý thuyết về đề tài nghiên cứu

Giữa hai biến định lượng có nhiều dạng liên hệ, có thể là tuyến tính hoặc phi tuyến hoặc không có bất kỳ một mối liên hệ nào. Thường các nhà nghiên cứu nhận diện sớm mối quan hệ một cặp biến thông qua đồ thị phân tán Scatter.

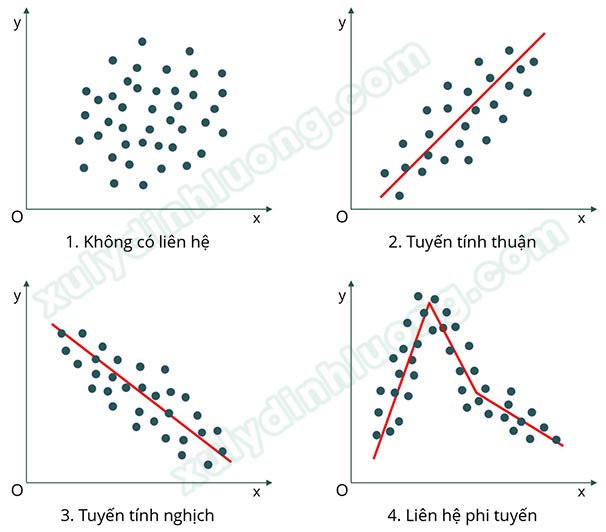
Hình 1, các điểm dữ liệu phân bố ngẫu nhiên không đi theo quy luật nào, hai biến này không có mối liên hệ với nhau. Hình 2, các điểm dữ liệu có xu hướng tạo thành một đường thẳng dốc lên, hai biến này có mối liên hệ tuyến tính thuận. Hình 3, các điểm dữ liệu có xu hướng tạo thành một đường thẳng dốc xuống, hai biến này có mối liên hệ tuyến tính nghịch. Hình 4, các điểm dữ liệu có xu hướng tạo thành các đường thẳng gấp khúc chứ không theo một hướng duy nhất, hai biến này có mối liên hệ phi tuyến.

2. Tương quan tuyến tính Pearson

Tương quan tuyến tính giữa hai biến là mối tương quan mà khi biểu diễn giá trị quan sát của hai biến trên mặt phẳng Oxy, các điểm dữ liệu có xu hướng tạo thành một đường thẳng. Theo Gayen (1951)[1], trong thống kê, các nhà nghiên cứu sử dụng hệ số tương quan Pearson (ký hiệu r) để lượng hóa mức độ chặt chẽ của mối liên hệ tuyến tính giữa hai biến định lượng. Nếu một trong hai hoặc cả hai biến không phải là biến định lượng (biến định tính, biến nhị phân,…) chúng ta sẽ không thực hiện phân tích tương quan Pearson cho các biến này. Hệ số tương quan Pearson r có giá trị dao động từ -1 đến 1:

Andy Field (2009) cho rằng mặc dù có thể đánh giá mối liên hệ tuyến tính giữa hai biến qua hệ số tương quan Pearson, nhưng chúng ta cần thực hiện kiểm định giả thuyết hệ số tương quan này có ý nghĩa thống kê hay không. Giả thuyết được đặt ra H₀: r = 0. Phép kiểm định t được sử dụng để kiểm định giả thuyết này. Kết quả kiểm định:

• Sig < 0.05: Bác bỏ giả thuyết H₀, nghĩa là r ≠ 0 một cách có ý nghĩa thống kê, hai biến có tương quan tuyến tính với nhau.
• Sig > 0.05: Chấp nhận giả thuyết H₀, nghĩa là r = 0 một cách có ý nghĩa thống kê, hai biến không có tương quan tuyến tính với nhau.

Khi đã xác định hai biến có mối tương quan tuyến tính, chúng ta sẽ xét đến độ mạnh/yếu của mối tương quan này thông qua trị tuyệt đối của r. Theo Andy Field (2009):

• |r| < 0.1: mối tương quan rất yếu
• |r| < 0.3: mối tương quan yếu
• |r| < 0.5: mối tương quan trung bình
• |r| ≥ 0.5: mối tương quan mạnh

Việc đánh giá mối quan hệ tương quan giữa hai biến không chỉ duy nhất dựa vào các con số, bởi có khả năng xảy ra tình trạng tương quan giả. Hai biến định lượng có hệ số tương quan rất cao nhưng thực tế lại không có mối quan hệ nào cả. Việc xuất hiện tương quan cao giữa hai biến không có mối quan hệ đến từ sự ngẫu nhiên trong xu hướng dữ liệu của mẫu hoặc một kết quả tình cờ từ một nguyên nhân chung nào đó. Ví dụ, kết quả tương quan Pearson cho thấy thu nhập trung bình đầu người tại Việt Nam và số lượng thiên tai qua các năm có sự tương quan thuận với nhau, chúng ta có thể đánh giá rằng đây là một kết quả tình cờ.

Mối liên hệ tương quan tuyến tính khác với liên hệ nhân quả. Để đánh giá sự tương quan tuyến tính giữa một cặp biến, chúng ta dùng phân tích tương quan Pearson. Nhưng để đánh giá mối liên hệ nhân quả, biến A thay đổi gây ra kết quả gì cho biến B, chúng ta cần sử dụng đến hồi quy. Nên nhớ rằng, không phải lúc nào hai biến có mối quan hệ tương quan thì giữa chúng cũng có mối liên hệ nhân quả với nhau. Ví dụ, lợi nhuận kinh doanh có sự tương quan chặt chẽ với số chi nhánh của nhà hàng, nhưng việc tăng số chi nhánh không phải lúc nào cũng làm tăng cao lợi nhuận. Lợi nhuận tăng sau khi nhà hàng mở thêm chi nhánh có thể là do sự tăng lên số lượng chi nhánh mới nhưng cũng có thể là do hiệu quả từ chiến dịch marketing rầm rộ, do sự tối ưu chi phí đầu vào… Thậm chí, việc tăng số chi nhánh còn chẳng tác động gì đến lợi nhuận, hoặc mức độ tác động đến lợi nhuận không lớn như hệ số tương quan r thể hiện.

3. Phân tích tương quan tuyến tính Pearson trên SPSS 26

Nếu đã mua Ebook SPSS 26, các bạn sử dụng tập dữ liệu có tên 350 – DLTH 1.sav để thực hành tương ứng với mô hình nghiên cứu và bảng câu hỏi khảo sát ở chương LÝ THUYẾT ĐỀ TÀI NGHIÊN CỨU – ĐỀ TÀI THỰC HÀNH. Sau bước phân tích nhân tố khám phá EFA, chúng ta có 7 biến đại diện được tạo ra để sử dụng cho phân tích tương quan Pearson. Thực hiện phân tích tương quan để đánh giá mối quan hệ giữa các biến bằng cách vào Analyze > Correlate > Bivariate…

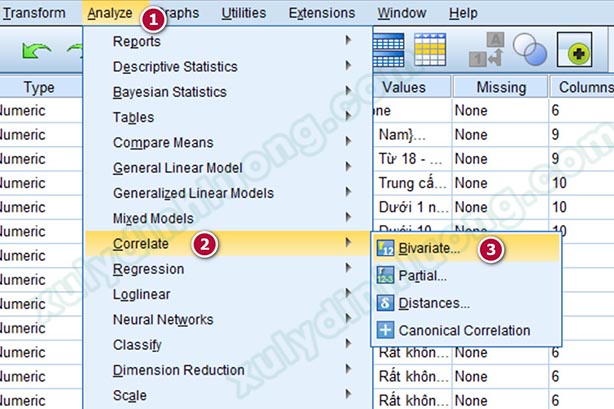
Tại đây, chúng ta đưa hết tất cả các biến muốn chạy tương quan Pearson vào mục Variables, cụ thể là các biến đại diện được tạo ra sau bước phân tích EFA. Để tiện cho việc đọc kết quả, chúng ta nên đưa biến phụ thuộc lên trên cùng. Nhấp vào OK để xác nhận thực hiện lệnh.

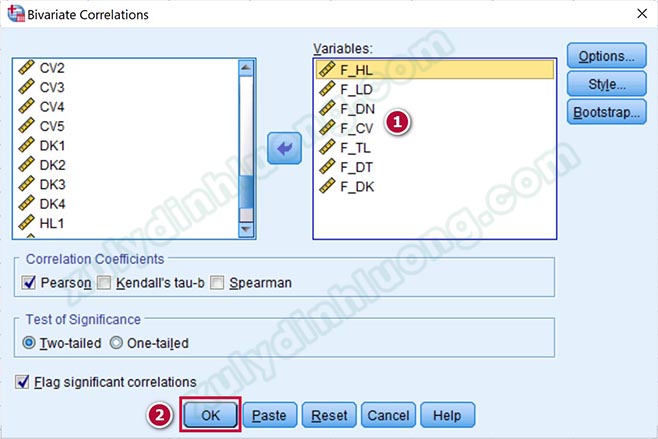
Kết quả tương quan Pearson sẽ được thể hiện trong bảng Correlations. Điểm qua các ký hiệu trong bảng này: Pearson Correlation là hệ số tương quan Pearson (r), Sig. (2-tailed) là giá trị sig của kiểm định t đánh giá hệ số tương quan Pearson có ý nghĩa thống kê hay không, N là cỡ mẫu.

4. Đọc kết quả tương quan Pearson trên SPSS

Chúng ta sẽ xem xét hai loại mối quan hệ tương quan: tương quan giữa biến phụ thuộc với các biến độc lập và tương quan giữa các biến độc lập với nhau. Sở dĩ việc chia ra như vậy, vì sự kỳ vọng về kết quả sẽ có đôi chút khác biệt giữa hai loại mối quan hệ này. Với sự tương quan giữa các biến độc lập với biến phụ thuộc, khi xây dựng mô hình nghiên cứu chúng ta đã tìm hiểu rất kỹ để tìm ra các biến độc lập có sự tác động lên biến phụ thuộc. Việc đưa ra các biến độc lập này dựa trên nền tảng cơ sở lý thuyết, các nghiên cứu tương tự trước đó và sự đánh giá tình hình thực tế tại môi trường khảo sát. Do đó, chúng ta kỳ vọng rằng kết quả phân tích từ dữ liệu sẽ cho thấy các biến độc lập có sự tương quan với biến phụ thuộc hoặc có sự tác động lên biến phụ thuộc. Nếu chúng ta thực hiện phân tích tương quan trước hồi quy, kết quả từ tương quan Pearson cho thấy biến độc lập có tương quan với biến phụ thuộc, khả năng biến độc lập đó sẽ tác động lên biến phụ thuộc ở hồi quy sẽ cao hơn.

Loại quan hệ thứ hai là tương quan giữa các biến độc lập với nhau. Tên gọi “biến độc lập” phần nào nói lên được đặc điểm kỳ vọng của dạng biến này: chúng độc lập về ý nghĩa với nhau. Giữa hai biến độc lập nếu có sự tương quan quá mạnh, có khả năng hai biến này bản chất chỉ là một biến, một khái niệm. Nếu hai hay nhiều biến độc lập tương quan mạnh với nhau cùng tham gia vào một phép hồi quy sẽ dễ dẫn đến hiện tượng cộng tuyến/đa cộng tuyến gây sai lệch kết quả thống kê (xem chi tiết hiện tượng cộng tuyến/đa cộng tuyến ở chương HỒI QUY TUYẾN TÍNH LINEAR REGRESSION trong Ebook SPSS 26). Do đó, chúng ta kỳ vọng rằng không có sự tương quan quá mạnh giữa các biến độc lập. Khi đồng thời sig kiểm định t của hai biến độc lập nhỏ hơn 0.05 và trị tuyệt đối hệ số tương quan Pearson giữa chúng lớn hơn 0.7, chúng ta cần hết sức lưu ý đến cặp biến này để đưa ra hướng xử lý trong trường hợp xảy ra tình trạng cộng tuyến/đa cộng tuyến.

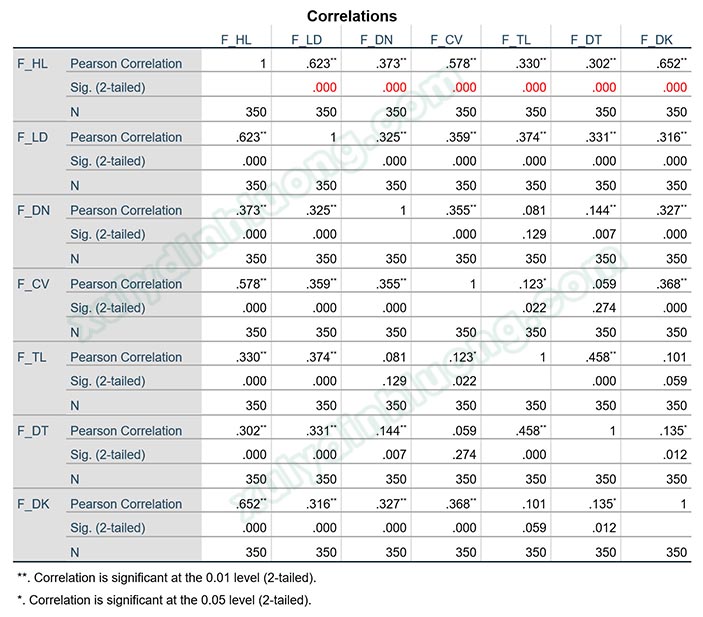
Quay lại với kết quả tương quan Pearson từ ví dụ ở trên, sig kiểm định t tương quan Pearson các giữa sáu biến độc lập F_LD, F_DN, F_CV, F_TL, F_DT, F_DK với biến phụ thuộc F_HL đều nhỏ hơn 0.05. Như vậy, có mối liên hệ tuyến tính giữa các biến độc lập này với biến phụ thuộc. Giữa các biến độc lập, không có mối tương quan nào quá mạnh khi trị tuyệt đối hệ số tương quan giữa các cặp biến đều nhỏ hơn 0.5, như vậy khả năng xảy ra hiện tượng cộng tuyến/đa cộng tuyến cũng thấp hơn.

[1] Gayen, The frequency distribution of the product-moment correlation coefficient in random samples of any size drawn from non-normal universes, Biometrika, 1951.