Trong hồi quy tuyến tính, toàn bộ biến thiên quan sát được của biến phụ thuộc được chia làm hai phần: phần biến thiên do hồi quy (gây ra bởi các biến độc lập) được biểu thị bằng R2 và phần biến thiên do phần dư (residual) gây ra. Chúng ta sẽ tìm hiểu chi tiết hai khái niệm này.

1. Độ phù hợp của mô hình
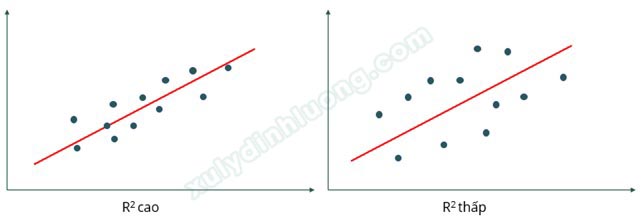
Các điểm dữ liệu luôn phân tán và có xu hướng tạo thành dạng một đường thẳng chứ không phải là một đường thẳng hoàn toàn. Do đó, hầu như không có đường thẳng nào có thể đi qua toàn bộ tất cả các điểm dữ liệu, luôn có sự sai lệch giữa các giá trị ước tính và các giá trị thực tế. Chúng ta sẽ cần tính toán được mức độ sai lệch đó cũng như mức độ phù hợp của mô hình hồi quy tuyến tính với tập dữ liệu. Một thước đo sự phù hợp của mô hình hồi quy tuyến tính thường dùng là hệ số xác định R2 (R square). Khi phần lớn các điểm dữ liệu tập trung sát vào đường hồi quy, giá trị R2 sẽ cao, ngược lại, nếu các điểm dữ liệu phân bố rải rác cách xa đường hồi quy, R2 sẽ thấp.
Khi chúng ta đưa thêm biến độc lập vào phân tích hồi quy, R2 có xu hướng tăng lên. Điều này dẫn đến một số trường hợp mức độ phù hợp của mô hình hồi quy bị thổi phồng khi chúng ta đưa vào các biến độc lập giải thích rất yếu hoặc không giải thích cho biến phụ thuộc. Trong SPSS, bên cạnh chỉ số R2, chúng ta còn có thêm chỉ số R2 Adjusted (R2 hiệu chỉnh). Chỉ số R2 hiệu chỉnh không nhất thiết tăng lên khi nhiều biến độc lập được thêm vào hồi quy, do đó R2 hiệu chỉnh phản ánh độ phù hợp của mô hình chính xác hơn hệ số R2.
R2 hay R2 hiệu chỉnh đều có mức dao động trong đoạn từ 0 đến 1. Nếu R2 càng tiến về 1, các biến độc lập giải thích càng nhiều cho biến phụ thuộc, và ngược lại, R2 càng tiến về 0, các biến độc lập giải thích càng ít cho biến phụ thuộc. Ví dụ, một mô hình hồi quy với biến phụ thuộc Y và hai biến độc lập: X1, X2 cho ra giá trị R2 hiệu chỉnh là 0.40. Điều này có nghĩa, hai biến độc lập đưa vào phân tích hồi quy giải thích được 40% sự biến thiên của biến phụ thuộc, 60% còn lại được giải thích bởi phần dư gồm các biến độc lập ngoài mô hình và sai số ngẫu nhiên.
Không có tiêu chuẩn chính xác R2 ở mức bao nhiêu thì mô hình mới đạt yêu cầu. Cần lưu ý rằng, không phải luôn luôn một mô hình hồi quy có R2 cao thì nghiên cứu có giá trị cao, mô hình có R2 thấp thì nghiên cứu đó có giá trị thấp, độ phù hợp mô hình hồi quy không có mối quan hệ nhân quả với giá trị của bài nghiên cứu. Trong nghiên cứu lặp lại, chúng ta thường chọn mức trung gian là 0.5 để phân ra 2 nhánh ý nghĩa mạnh/ý nghĩa yếu và kỳ vọng từ 0.5 đến 1 thì mô hình là tốt, bé hơn 0.5 là mô hình chưa tốt. Tuy nhiên, điều này không thực sự chính xác bởi việc đánh giá giá trị R2 sẽ phụ thuộc rất nhiều vào các yếu tố như lĩnh vực nghiên cứu, tính chất nghiên cứu, cỡ mẫu, số lượng biến tham gia hồi quy, kết quả các chỉ số khác của phép hồi quy,…
Chúng ta cần đánh giá độ phù hợp mô hình một cách chính xác qua kiểm định giả thuyết. Để kiểm định độ phù hợp mô hình hồi quy, chúng ta đặt giả thuyết H0: R2 = 0. Phép kiểm định F được sử dụng để kiểm định giả thuyết này. Kết quả kiểm định:
- Sig < 0.05: Bác bỏ giả thuyết H0, nghĩa là R2 ≠ 0 một cách có ý nghĩa thống kê, mô hình hồi quy là phù hợp.
- Sig > 0.05: Chấp nhận giả thuyết H0, nghĩa là R2 = 0 một cách có ý nghĩa thống kê, mô hình hồi quy không phù hợp.
Trong SPSS, các số liệu của kiểm định F được lấy từ bảng phân tích phương sai ANOVA.
Nếu bạn gặp vấn đề với kiểm định độ phù hợp mô hình hồi quy như sig kiểm định F lớn hơn 0.05, R bình phương mang giá trị âm hoặc quá thấp đến mức mô hình không có ý nghĩa, có thể tham khảo dịch vụ chạy SPSS thuê từ Xử Lý Định Lượng nhé.
2. Phần dư
Như đã đề cập ở trên, đường hồi quy không thể đi qua toàn bộ các điểm dữ liệu, sẽ có những điểm nằm ngoài đường hồi quy. Khoảng cách từ mỗi điểm dữ liệu đến đường hồi quy được coi là phần dư ε trong hồi quy (nếu trên dữ liệu tổng thể gọi là sai số). Khoảng cách này càng lớn thì phần dư càng cao. Phần dư lớn đồng nghĩa R2 sẽ nhỏ, mô hình hồi quy càng ít có ý nghĩa.

Hầu hết các dữ liệu không phù hợp tuyệt đối với đường hồi quy mà sẽ luôn tồn tại phần dư đi đôi. Điều này là hoàn toàn dễ hiểu trên thực tế, bởi việc chúng ta tìm được các biến độc lập giải thích được toàn bộ biến thiên của biến phụ thuộc là điều không thể xảy ra. Tuy nhiên, phần dư không nên quá lớn, bởi phần dư càng lớn các biến độc lập đưa vào phân tích hồi quy càng mang ít ý nghĩa, chúng ta sẽ không tìm được thông tin hữu ích từ kết quả phân tích hồi quy.












