Ký hiệu mũi tên hai chiều trong AMOS (↔) được phần mềm đặt tên là Draw Covariances (Double Headed Arrows). Mũi tên này hầu như sẽ được sử dụng trong hai trường hợp chính: (1) biểu diễn sự tương quan của các biến đóng vai trò độc lập và (2) nối các sai số có chỉ số hiệu chỉnh MI (Modification Indices) cao để cải thiện độ phù hợp mô hình.
1. Mũi tên hai chiều biểu diễn mối tương quan (correlation) giữa các biến độc lập với nhau
Trong SEM, tính xác định (identification) của mô hình là rất quan trọng. Tính xác định của mô hình nghĩa là mô hình đó vẽ ra được, chạy phân tích được, kết quả không xuất hiện lỗi và phù hợp với dữ liệu. Một mô hình không được xác định khi phân tích trên AMOS thường sẽ không thể thực hiện được và phần mềm sẽ báo lỗi.
Barbara M. Byrne (2009) trong cuốn Structural Equation Modeling With AMOS đã nói rằng: If a unique solution for the values of the structural parameters can be found, the model is considered to be identified, tạm dịch: Nếu giá trị của các tham số cấu trúc của mô hình tìm ra là duy nhất, mô hình được coi là đã được xác định. Như vậy, việc khai báo các tham số chính xác trong mô hình là cực kỳ quan trọng để giúp mô hình có thể xác định được.
Cũng theo Barbara M. Byrne (2009), mỗi tương quan giữa các biến độc lập trong mô hình là một tham số. Do đó, khi vẽ mô hình SEM/CFA trên AMOS, chúng ta cần nối mũi tên hai chiều giữa các biến độc lập lại với nhau để khai báo cho phần mềm biết rằng đó là một tham số cần ước lượng. Mũi tên này sẽ khai báo cho phần mềm biết về sự tồn tại tương quan (correlation) giữa các biến độc lập với nhau. Với CFA, chúng ta không đánh giá mối quan hệ tác động nhân quả, nên không phân biệt độc lập với phụ thuộc trong mô hình, chúng ta sẽ xem tất cả các biến tiềm ẩn (độc lập lẫn phụ thuộc) đều là độc lập. Với SEM, bên cạnh mối tác động nhân quả (mũi tên một chiều từ độc lập lên phụ thuộc), mũi tên hai chiều nối các biến độc lập với nhau đóng vai trò hết sức quan trọng khi xét cả sự tương quan giữa các biến độc lập với nhau trong lúc xét mối tác động nhân quả. Nếu không vẽ mũi tên hai chiều giữa các biến độc lập trong SEM, nghĩa là chỉ tồn tại mối tác động nhân quả và không hề tồn tại sự tương quan nào giữa các biến độc lập.
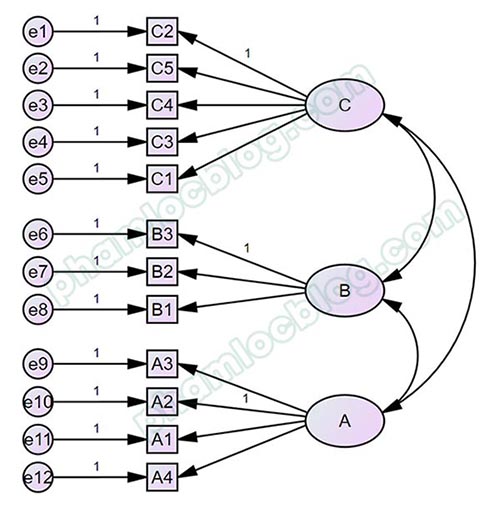
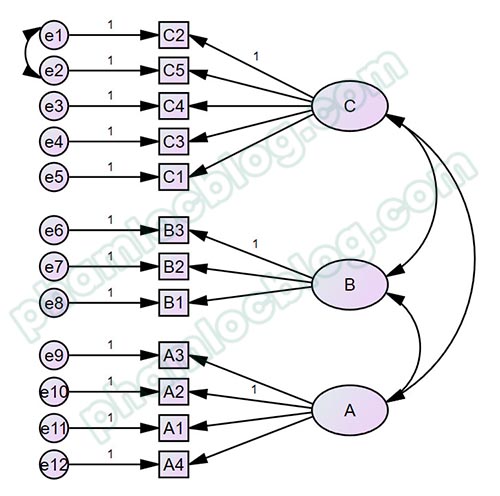
Trong hình ảnh bên trên, 3 biến A, B, C là các biến tiềm ẩn độc lập, các biến này được nối mũi tên hai chiều với nhau. Giả sử chúng ta không nỗi mũi tên giữa biến A và C, khi thực hiện phân tích, một thông báo sẽ xuất hiện như bên dưới để chúng ta xác nhận có nối mũi tên giữa A với C không.
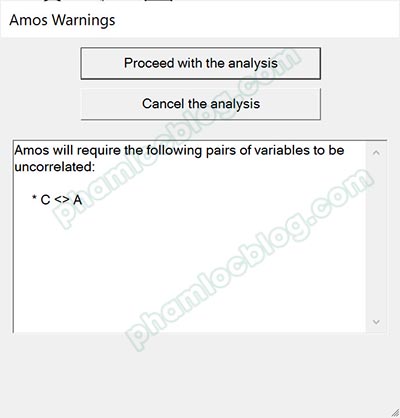
Chúng ta có hai lựa chọn, hoặc là chọn Proceed with the analysis để yêu cầu phần mềm vẫn thực hiện phân tích hoặc chọn Cancel the analysis và bổ sung mũi tên hai chiều nối A với C, sau đó thực hiện phân tích lại. Cả hai lựa chọn đều cho ra được kết quả, tuy nhiên kết quả lại không giống nhau.
Ở đây, mặc dù chúng ta khai báo thiếu tham số tương quan giữa các biến độc lập, nhưng AMOS vẫn cho phép chúng ta thực hiện, bởi vì tham số này không phải là tham số bắt buộc để mô hình được xác định. Tuy nhiên, lúc này có khả năng các tham số ước lượng của mô hình không phải là duy nhất, điều này không hề tốt trong đại đa số các trường hợp.
Tóm lại, ở mục này, chúng ta cần lưu ý, với các biến độc lập, chúng ta cần vẽ mũi tên hai chiều nối chúng lại với nhau. Mũi tên này nhằm mục đích khai báo cho phần mềm về việc tồn tại sự tương quan (correlation) giữa các biến độc lập.
2. Mũi tên hai chiều nối các cặp sai số có MI cao
AMOS cung cấp cho chúng ta có một chỉ số gọi là chỉ số hiệu chỉnh MI (Modification Indices). Chỉ số này cao chỉ ra các vấn đề về cấu trúc thang đo nhân tố, trùng lắp thang đo, làm giảm độ phù hợp mô hình. Bảng Covariances trong MI thể hiện vấn đề hiệp phương sai của các yếu tố với nhau. Chúng ta sẽ chú trọng tới hiệp phương sai cặp sai số e trong cùng một thang đo. Không có tiêu chuẩn nhất định nào về ngưỡng MI bao nhiêu là cao, tuy nhiên thường các nhà nghiên cứu chọn mức trên 30 làm ngưỡng cân nhắc để đưa ra hướng hiệu chỉnh mô hình.
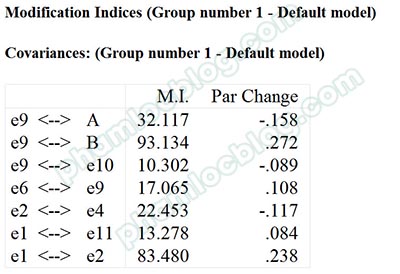
Kết quả MI Covariances ở trên cho thấy cặp sai số e1 và e2 có MI rất cao là 83.480, và 2 sai số này tương ứng với biến quan sát C2, C5 thuộc cùng thang đo C. MI cao chỉ ra rằng nếu nối mũi tên hai chiều cặp sai số này thì hệ số MI sẽ giảm và mô hình sẽ tốt hơn. Thường việc dẫn đến MI cao giữa hai sai số của hai biến quan sát cùng một thang đo là do sự chồng chéo, trùng lặp dữ liệu (hai câu hỏi có nội dung tương tự nhau).
Để giảm MI và tăng độ phù hợp mô hình, chúng ta cần khai báo cho phần mềm biết rằng cặp e1-e2 có hiệp phương sai cao bằng cách nối mũi tên hai chiều giữa chúng.
Sau khi đã nối mũi tên hai chiều nối hiệp phương sai giữa hai sai số với nhau, chúng ta thực hiện phân tích lại. Nếu tiếp tục xuất hiện các cặp sai số của các biến quan sát cùng thang đo có MI cao, chúng lại tiếp tục nối mũi tên hai chiều giữa chúng và phân tích lại đến khi không còn chỉ số MI nào cao khác biệt nữa.












