Kết quả phân tích hồi quy đa biến trong SPSS chúng ta sẽ có được các bảng kết quả quan trọng để đánh giá kết quả hồi quy. Một trong những bảng đó là Coefficients với nhiều giá trị quan trọng như sig kiểm định t, giá trị VIF, hệ số hồi quy. Bảng này có 2 cột hệ số hồi quy là B (chưa chuẩn hóa) và Beta (đã chuẩn hóa), vậy chúng ta sẽ sử dụng cột nào và sự khác nhau giữa 2 hệ số hồi quy này ra sao? Cùng Xử Lý Định Lượng tìm hiểu chi tiết về cách dùng 2 hệ số hồi quy này nhé.

1. Tiêu chuẩn chung khi viết phương trình hồi quy trên SPSS
Khi viết phương trình hồi quy, kể cả chuẩn hóa hay chưa chuẩn hóa đi nữa, chúng ta trước hết cần đảm bảo các tiêu chuẩn chung về mặt thống kê như sau:
– Phương trình hồi quy luôn luôn có phần dư (sai số) ở cuối phương trình:
Y = B0 + B1X1 + B2X2 + … + BiXi + 𝜀
Y = Beta1X1 + Beta2X2 + … + BetaiXi + 𝜀
– Chỉ đưa vào phương trình hồi quy những biến có ý nghĩa thống kê. Giả sử chúng ta lấy mức ý nghĩa phép kiểm định t hồi quy là 5% (0.05), khi biến độc lập A từ bảng Coefficients có giá trị sig = 0.08 > 0.05, nghĩa là biến này không có ý nghĩa thống kê. Khi viết phương trình, không đưa biến độc lập A vào.
– Không có quy định thống nhất về việc nên viết phương trình nào bởi mỗi phương trình đều có ý nghĩa riêng. Do vậy, tùy mục đích của chúng ta mà đưa phương trình phù hợp. Với các đề tài về mảng kinh tế, tiếp thị (marketing), quản trị doanh nghiệp, thường các nhà nghiên cứu sử dụng phương trình hồi quy chuẩn hóa để so sánh tầm quan trọng giữa các biến độc lập.
– Thứ tự các biến đưa vào hồi quy không ảnh hưởng đến các chỉ số hồi quy của biến trong bảng Coefficients, do vậy, tùy ý chúng ta sắp xếp vị trí biến.
2. Khác biệt phương trình hồi quy chuẩn hóa và chưa chuẩn hóa
2.1 Hệ số hồi quy chưa chuẩn hóa B
Đây là hệ số hồi quy chúng ta sử dụng phổ biến để viết phương trình hồi quy. Chúng ta không nhận xét thứ tự tác động của các biến độc lập lên biến phụ thuộc dựa vào hệ số hồi quy chưa chuẩn hóa bởi các biến độc lập không đồng nhất về đơn vị hoặc nếu đồng nhất về đơn vị thì độ lệch chuẩn các biến cũng là khác nhau. Phương trình hồi quy chưa chuẩn hóa có dạng:
Y = B0 + B1X1 + B2X2 + … + BiXi + 𝜀
Đối với phương trình dạng này, các hệ số hồi quy phản ánh sự thay đổi của biến phụ thuộc khi một biến độc lập thay đổi và các biến độc lập còn lại được giữ nguyên. Khi nhận xét chúng ta sẽ dùng cụm câu sau: Trong điều kiện các biến khác không thay đổi giá trị, khi X1 thay đổi 1 đơn vị, Y sẽ thay đổi B1 đơn vị.
Ví dụ: Giả sử, biến Y là biến Tốc độ chạy của xe (km/h), biến X1 là biến Khối lượng của xe (kg), biến X2 là Đường kính bánh xe (cm) … Các biến độc lập Khối lượng của xe, Đường kính bánh xe sẽ tác động đến Tốc độ chạy của xe (X1, X2…. tác động đến Y). Khi đó chúng ta sẽ diễn giải hàm ý quản trị như sau:
– Trong điều kiện các biến khác không thay đổi, khi khối lượng của xe (biến X1) thay đổi 1kg thì tốc độ chạy của xe (Y) thay đổi B1 km/h.
– Trong điều kiện các biến khác không thay đổi, khi đường kính bánh xe (biến X2) thay đổi 1cm thì tốc độ chạy của xe (Y) thay đổi B2 km/h.
Chữ “thay đổi” trong câu nhận xét sẽ tùy trường hợp hệ số hồi quy dương hay âm mà chuyển thành “tăng” và “giảm”.
Ở ví dụ trên đây, thực tế chúng ta thấy rằng, khối lượng xe tăng làm xe chạy chậm hơn, nghĩa là hệ số hồi quy B1 âm (tương quan nghịch, X giảm Y tăng, X tăng Y giảm). Chính vì vậy, câu nhận xét sẽ sửa lại: “Trong điều kiện các biến khác không thay đổi, khi khối lượng của xe (biến X1) tăng 1kg thì tốc độ chạy của xe (Y) giảm B1 km/h”.
Ngược lại, trên thực tế, đường kính bánh xe tăng sẽ làm xe chạy nhanh hơn, nghĩa là hệ số hồi quy B2 dương (tương quan thuận, X tăng Y tăng, X giảm, Y giảm). Chính vì vậy, câu nhận xét sẽ sửa lại: “Trong điều kiện các biến khác không thay đổi, khi đường kính bánh xe (biến X2) tăng 1cm thì tốc độ chạy của xe (Y) tăng B2 km/h”.
2.2 Hệ số hồi quy chuẩn hóa Beta
Đây là hệ số hồi quy chúng ta sử dụng phổ biến để kết luận thứ tự tác động của các biến độc lập lên biến phụ thuộc nhờ sự đồng nhất về đơn vị và độ lệch chuẩn các biến tham gia vào mô hình hồi quy. Phương trình hồi quy chuẩn hóa có dạng:
Y = Beta1X1 + Beta2X2 + … + BetaiXi + 𝜀
Từ phương trình hồi quy chuẩn hóa, chúng ta sẽ biết được biến X nào ảnh hưởng mạnh hay yếu đến biến Y căn cứ vào trị tuyệt đối của hệ số hồi quy chuẩn hóa, trị tuyệt đối hệ số Beta càng lớn thì tầm quan trọng của biến đối với Y càng lớn.
Hệ số hồi quy kể cả B hay Beta khi mang dấu dương nghĩa là biến độc lập tác động thuận chiều với biến phụ thuộc, hệ số hồi quy mang dấu âm nghĩa là biến độc lập tác động nghịch chiều với biến phụ thuộc.
Với dạng đề tài sử dụng thang đo Likert, các bạn nên ưu tiên sử dụng phương trình hồi quy chuẩn hóa để kết luận để có thể diễn giải hàm ý quản trị nhiều hơn.
Ví dụ: Dưới đây là bảng Coefficients từ kết quả hồi quy với biến phụ thuộc là HL – Sự hài lòng của nhân viên, các biến độc lập là:
- Lương, thưởng, phúc lợi: TN
- Bản chất công việc: CV
- Quan hệ với lãnh đạo: LD
- Môi trường làm việc: MT
- Đào tạo và thăng tiến: DT
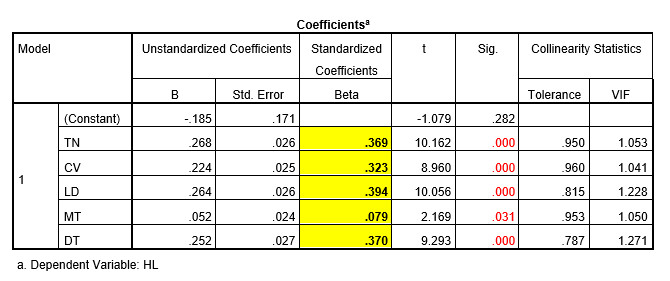
Phương trình hồi quy chuẩn hóa:
HL = 0.394*LD + 0.370*DT + 0.369*TN + 0.323*CV + 0.079*MT + e
Sự hài lòng của nhân viên = 0.394 * Lãnh đạo và cấp trên
+ 0.370 * Cơ hội đào tạo và thăng tiến
+ 0.369 * Lương, thưởng, phúc lợi
+ 0.323 * Bản chất công việc
+ 0.079 * Điều kiện làm việc
Dựa vào độ lớn của hệ số hồi quy chuẩn hóa Beta, thứ tự mức độ tác động từ mạnh nhất tới yếu nhất của các biến độc lập tới biến phụ thuộc HL là: LD (0.394) > DT(0.370) > TN (0.369) > CV (0.323) > MT (0.079). Tương ứng với:
- Biến Lãnh đạo và cấp trên tác động mạnh nhất tới sự hài lòng của nhân viên.
- Biến Cơ hội đào tạo và thăng tiến tác động mạnh thứ 2 tới sự hài lòng của nhân viên.
- Biến Lương, thưởng, phúc lợi tác động mạnh thứ 3 tới sự hài lòng của nhân viên.
- Biến Bản chất công việc tác động mạnh thứ 4 tới sự hài lòng của nhân viên.
- Biến Điều kiện làm việc tác động yếu nhất tới sự hài lòng của nhân viên.
Nếu bạn gặp khó khăn khi kết quả hồi quy không có ý nghĩa, giá trị R2 quá thấp, các biến độc lập bị loại nhiều, vi phạm đa cộng tuyến, vi phạm các giả định hồi quy. Bạn có thể tham khảo dịch vụ xử lý số liệu SPSS của Xử Lý Định Lượng để team có thể hỗ trợ bạn xử lý nhanh và hiệu quả nhất.












