Hệ số Q2 Predict – Đánh giá khả năng dự báo ngoài mẫu trong SMARTPLS 4

Trong PLS-SEM, chỉ số Q2 Predict (Q Square) là thước đo quan trọng để kiểm tra khả năng dự đoán (predictive relevance) của mô hình đối với dữ liệu mới (ngoài mẫu – out-of-sample). Nói cách khác, nó cho biết mô hình bạn xây dựng có thể dự đoán tốt dữ liệu chưa từng được sử dụng để ước lượng hay không.

1. Năng lực dự báo và hệ số Q2 predict trong SMARTPLS 4

1.1 Khái niệm cơ bản

• Dữ liệu trong mẫu (in-sample): là toàn bộ dữ liệu đã thu thập được và dùng trực tiếp để chạy mô hình. Các chỉ số như R², hệ số đường dẫn… đều được tính trên tập dữ liệu này.

• Dữ liệu ngoài mẫu (out-of-sample): là dữ liệu mới, chưa được sử dụng để xây dựng mô hình. Trong thực tế, cần thu thập thêm để kiểm chứng, nhưng trong SMARTPLS 4, việc này được mô phỏng bằng PLSpredict (kỹ thuật giả lập dữ liệu ngoài mẫu).

Vấn đề: R² chỉ phản ánh khả năng giải thích dữ liệu hiện có, nhưng không đảm bảo mô hình sẽ dự đoán chính xác khi gặp dữ liệu mới. Q² Predict giải quyết điểm hạn chế này.

1.2 Cách tính Q2 Predict trong SMARTPLS 4

SMARTPLS 4 sử dụng kỹ thuật cross-validation (k-fold) để mô phỏng dữ liệu ngoài mẫu:

Bước 1: Chia dữ liệu (ví dụ 300 quan sát) thành nhiều phần nhỏ (k folds).

Bước 2: Ở mỗi vòng lặp:

• Lấy tập huấn luyện (ví dụ 270 mẫu) để chạy mô hình.
• Giữ lại tập kiểm tra (ví dụ 30 mẫu) làm dữ liệu “ngoài mẫu”.
• Dùng mô hình huấn luyện để dự đoán giá trị của 30 mẫu này.
• So sánh giá trị dự đoán với giá trị thực để tính sai số.

Bước 3: Lặp lại cho đến khi toàn bộ dữ liệu đều lần lượt được dùng làm “ngoài mẫu”.

Bước 4: Kết quả dự đoán được tổng hợp lại → tính hệ số Q² Predict.

1.3 Ý nghĩa của Q² Predict

Q² Predict cho thấy mức độ chính xác của mô hình khi áp dụng cho dữ liệu mới. “Dự báo” ở đây không có nghĩa là dự báo tương lai theo thời gian, mà là dự đoán cho những quan sát chưa từng được dùng để xây dựng mô hình. Một mô hình có R² cao chưa chắc đã có Q² Predict cao. Ngược lại, Q² Predict mới phản ánh giá trị thực tiễn của mô hình trong việc dự đoán hành vi/biến số của các đối tượng mới.

1.4 Ví dụ minh họa (SERVQUAL → Sự hài lòng)

Nghiên cứu sử dụng 300 mẫu để kiểm tra ảnh hưởng của 5 yếu tố SERVQUAL đến sự hài lòng khách hàng.

Kết quả in-sample: R² = 0.65, tức mô hình giải thích 65% biến thiên của sự hài lòng trong 300 mẫu này.

Khi chạy PLSpredict: SMARTPLS chia nhỏ 300 mẫu, liên tục dự đoán trên tập kiểm tra.

Q² Predict thu được cho thấy mô hình có dự báo chính xác (hoặc không) với khách hàng mới chưa nằm trong tập 300 mẫu ban đầu.

2. Cốt lõi của Q2 predict

Bản chất của việc đánh giá Q² Predict là so sánh hiệu quả dự báo của mô hình PLS-SEM với một mô hình tham chiếu đơn giản (benchmark model). Nếu mô hình PLS không dự đoán tốt hơn benchmark, thì nó không thực sự có giá trị dự báo.

2.1 Mô hình Benchmark (mốc so sánh)

Trong PLSpredict, benchmark là các mô hình “ngây thơ” (naïve models), dự báo dựa trên quy tắc rất cơ bản, không dùng cấu trúc PLS-SEM. Có hai loại benchmark chính:

• Indicator Average (IA – dự báo bằng trung bình):
  Mọi quan sát mới đều được dự đoán bằng giá trị trung bình của dữ liệu huấn luyện.
  Ví dụ: Nếu điểm trung bình “Sự hài lòng” trong 270 khách hàng training là 3.8, thì khách hàng mới sẽ được dự đoán có “Sự hài lòng = 3.8”.

• Linear Model (LM – mô hình hồi quy tuyến tính):
  Thay vì sử dụng cấu trúc PLS-SEM, LM hồi quy trực tiếp tất cả biến quan sát độc lập (exogenous indicators) lên từng biến quan sát phụ thuộc (endogenous indicators).
  Ví dụ: Dự đoán từng chỉ báo của “Sự hài lòng” bằng hồi quy tuyến tính từ tất cả chỉ báo của SERVQUAL.

Mục tiêu của benchmark: tạo ra “đối chứng” để kiểm chứng xem PLS-SEM có thật sự mang lại cải thiện về khả năng dự báo.

2.2 Mô hình PLS (PLS-SEM model)

Đây là mô hình bạn đã xây dựng trong SMARTPLS, với các biến tiềm ẩn (latent variables) được đo lường bằng nhiều biến quan sát và có mối quan hệ đường dẫn (path) giữa chúng. Mục tiêu của PLS-SEM là ước lượng các hệ số đường dẫn (β) giữa biến tiềm ẩn và dự đoán giá trị biến phụ thuộc dựa trên lý thuyết.

Ví dụ:

• PLS-SEM model: SERVQUAL (5 thành phần) → Sự hài lòng.

• Benchmark IA: luôn dự đoán “Sự hài lòng” bằng trung bình mẫu cũ.

• Benchmark LM: dự đoán các chỉ báo “Sự hài lòng” bằng hồi quy tuyến tính từ tất cả chỉ báo SERVQUAL, bỏ qua cấu trúc SERVQUAL → Sự hài lòng.

2.3 So sánh PLS vs. Benchmark

Trong thực tế, thường so sánh PLS-SEM với mô hình trung bình (IA), vì đây là mức kiểm chứng cơ bản nhất. Nếu mô hình PLS-SEM không dự đoán tốt hơn việc chỉ lấy trung bình, thì mô hình không có giá trị dự báo.

Cách diễn giải Q² Predict:

• Q² Predict > 0: sai số dự đoán của PLS nhỏ hơn benchmark → mô hình có giá trị dự báo.

• Q² Predict ≤ 0: PLS dự đoán tệ hơn hoặc không hơn gì benchmark → mô hình chỉ phù hợp dữ liệu cũ (in-sample), không hữu ích cho dữ liệu mới.

Ví dụ minh họa (SERVQUAL → Sự hài lòng, N = 300):

• Nếu Q² Predict = 0.45 (>0): mô hình dự báo tốt hơn benchmark, giá trị dự báo ở mức trung bình – cao.

• Nếu Q² Predict = ≤ 0: mô hình không hơn gì “đoán mò bằng trung bình”, tức chỉ giải thích được dữ liệu cũ, không có giá trị ngoài mẫu.

óm lại, cốt lõi của Q² Predict là kiểm chứng giá trị dự báo ngoài mẫu bằng cách so sánh PLS-SEM với benchmark. Chỉ khi PLS vượt qua benchmark (đặc biệt là IA), mô hình mới thực sự đáng tin cậy về khả năng dự báo.

3. Vì sao Q² Predict chỉ áp dụng cho biến phụ thuộc mà không áp dụng cho biến độc lập?

4. Phân tích Q2 Predict trong SMARTPLS 4

Giả sử ta có một mô hình nghiên cứu như hình minh họa, trong đó có hai biến phụ thuộc cần đánh giá Q2 Predict là NB và TT.

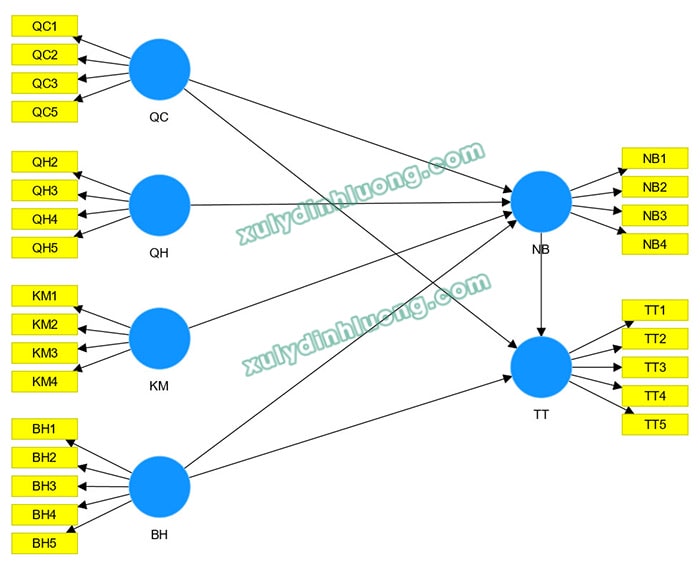
Lưu ý: SMARTPLS 3 không hỗ trợ PLS Predict. Chỉ từ SMARTPLS 4 trở đi bạn mới có thể chạy phân tích này (ở đây mình thực hành trên phiên bản 4.1.1.2). Bạn có thể mua phần mềm SMARPLS Pro full bản quyền vĩnh viễn tại đây.

Tạo giao diện phần mềm SMARTPLS 4, vào Calculate > PLSpredict/CVPAT.

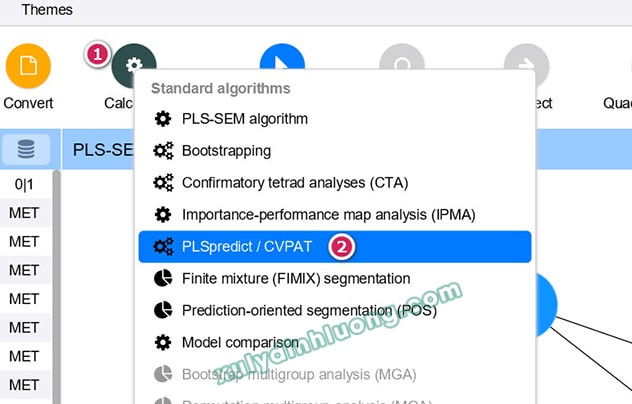
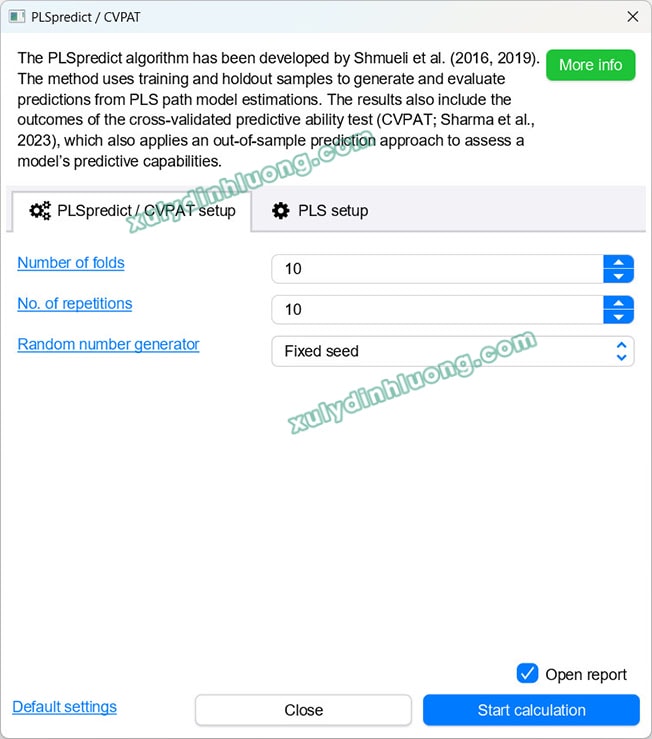
Khi cửa sổ thiết lập hiện ra, ta cấu hình các tham số cho quy trình cross-validation như sau:

1. Number of folds (số fold trong k-fold cross validation)

• Mặc định: 10 (tức 10-fold CV).

  • Dữ liệu chia thành 10 phần bằng nhau.

  • Mỗi lần lấy 9 phần để train, 1 phần để test.

  • Lặp lại 10 lần cho đến khi mọi quan sát đều từng được dự đoán trong test set.

• Khuyến nghị: từ 5 đến 15 folds là hợp lý.

2. No. of repetitions (số lần lặp k-fold CV)

• Mặc định: 10.

• Sau khi hoàn tất k-fold, phần mềm sẽ lặp lại quy trình nhiều lần với cách chia fold khác nhau. Điều này giúp kết quả ổn định, không phụ thuộc vào một lần chia ngẫu nhiên.

• Khuyến nghị: 5–10 repetitions thường đủ cho nghiên cứu học thuật. Nếu muốn kết quả “mượt” hơn (giảm ảnh hưởng của random split), có thể tăng lên 20–30, nhưng thời gian chạy sẽ lâu hơn.

3. Random number generator (bộ sinh số ngẫu nhiên)

• Fixed seed: dùng cùng một seed mỗi lần chạy → kết quả tái lập chính xác (phù hợp nghiên cứu khoa học).

• Random seed: mỗi lần chạy phần mềm tự chọn seed khác → kết quả có dao động nhỏ.

Nhìn chung, các thông số mặc định SMARTPLS 4 đã tối ưu, thường bạn chỉ cần giữ nguyên và bấm Start calculation.

Sau khi chạy xong, cửa sổ kết quả sẽ xuất hiện. Bạn tập trung vào 3 mục chính (được đánh số trong ảnh minh họa) để diễn giải Q² Predict và so sánh với benchmark.

5. Diễn giải kết quả Q2 Predict trong SMARTPLS 4

Ngưỡng đánh giá Q2 predict theo Hair và cộng sự (2022) nếu lớn hơn 0 là mô hình có khả năng dự báo. Nghiên cứu mới không còn chia ra các ngưỡng Q2 yếu, trung bình, mạnh như tài liệu cũ năm 2019 vì các ngưỡng này không thực sự chính xác. Do vậy, khi trình bày kết quả Q2 predict vào bài luận, bài nghiên cứu, bạn chi cần đảm bảo kết quả Q2 predict > 0 là được.

1. PLSpredict LV Summary (cấp biến tiềm ẩn)

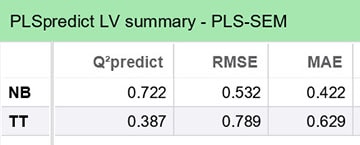
Đây là bảng thể hiện giá trị Q² Predict ở cấp độ latent variable – tức các biến phụ thuộc trong mô hình.

• NB: Q² Predict = 0.722 → rất cao, cho thấy mô hình có năng lực dự báo mạnh.

• TT: Q² Predict = 0.387 → dương và khá tốt, thể hiện năng lực dự báo ở mức trung bình – khá.

Cả hai biến NB và TT đều có Q² Predict > 0, nghĩa là mô hình có giá trị dự báo ngoài mẫu.

2. PLSpredict MV Summary (cấp biến quan sát)

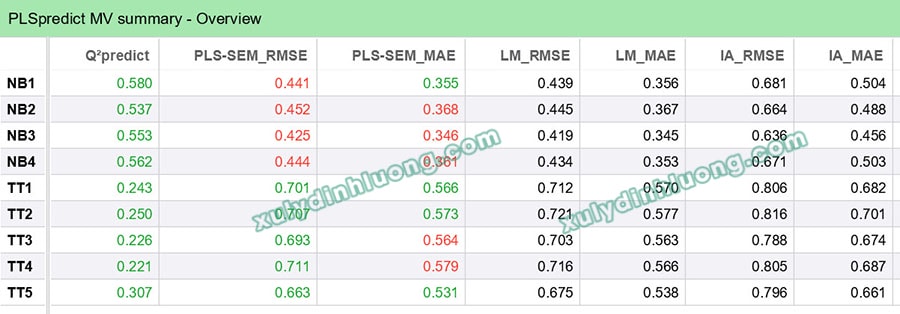
Bảng này cho biết kết quả dự báo ở cấp manifest variable (chỉ báo đo lường).

• Tất cả các chỉ báo NB1–NB4, TT1–TT5 đều có Q² Predict > 0 → mọi biến quan sát đều có giá trị dự báo.

• So sánh RMSE giữa mô hình PLS-SEM và benchmark (LM, IA):

  • NB1–NB4: RMSE PLS-SEM (0.425–0.452) < LM và IA → dự báo mạnh.

  • TT1–TT5: RMSE PLS-SEM (0.693–0.711) ≈ hoặc thấp hơn LM, và thấp hơn nhiều so với IA → dự báo hợp lý nhưng yếu hơn nhóm NB.

Kết luận: Nhóm NB có dự báo mạnh và ổn định, trong khi nhóm TT vẫn có dự báo nhưng kém hơn.

3. CVPAT LV Summary (so sánh PLS-SEM với Indicator Average – IA)

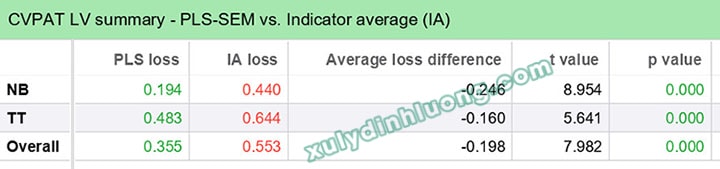
Bảng này kiểm định tổn thất dự đoán (prediction loss) của mô hình PLS-SEM so với benchmark IA.

• NB: PLS loss = 0.194 < IA loss = 0.440 → PLS-SEM vượt trội hơn nhiều so với baseline.

• TT: PLS loss = 0.483 < IA loss = 0.644 → PLS-SEM cũng tốt hơn baseline, nhưng khoảng cách nhỏ hơn so với NB.

 Giá trị p = 0.000 cho cả hai biến → sự khác biệt có ý nghĩa thống kê.

Tổng kết

• NB: dự báo mạnh, ổn định, vượt trội so với benchmark.

• TT: có dự báo ngoài mẫu, nhưng kém hơn NB.

• Mô hình PLS-SEM: chứng minh năng lực dự báo thực sự khi so sánh với baseline (IA).

——

Nguồn tham khảo:

Shmueli, G., Ray, S., Estrada, J. M. V., & Chatla, S. B. (2016). The Elephant in the Room: Predictive Performance of PLS Models. Journal of Business Research, 69(10), 4552-4564.

Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2022). A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM) (3 ed.). Thousand Oaks, CA: Sage

https://smartpls.com/documentation/algorithms-and-techniques/predict

https://github.com/ISS-Analytics/pls-predict