Với xu thế ứng dụng phần mềm trong nghiên cứu khoa học ngày càng nhiều như hiện nay, việc phân tích số liệu trở nên quan trọng hơn bao giờ hết. Phần mềm SPSS (Statistical Package for the Social Sciences) chính là một công cụ mạnh mẽ giúp người dùng thực hiện các phân tích thống kê, từ đơn giản đến phức tạp. Bài viết này sẽ cung cấp hướng dẫn cách chạy SPSS cho những ai mới bắt đầu tìm hiểu về phần mềm này.
1. Giới thiệu về giao diện phần mềm SPSS
Khi bạn lần đầu tiên tiếp xúc với phần mềm SPSS, có thể gặp nhiều khó khăn. Tuy nhiên, nếu bạn nắm rõ các bước cơ bản, việc sử dụng nó sẽ trở nên dễ dàng hơn. Đầu tiên, bạn hãy cài đặt phần mềm SPSS trên máy tính của mình.
Một khi đã hoàn tất cài đặt, bạn cần khởi động chương trình và làm quen với giao diện. Giao diện của SPSS khá thân thiện với người dùng, nhưng cũng đầy đủ chức năng để phục vụ cho việc phân tích dữ liệu. Để tải và cài đặt SPSS, bạn có thể chọn một phiên bản phù hợp tại bài viết này.
1.1 Khởi động phần mềm SPSS
Để bắt đầu, bạn cần mở phần mềm SPSS đã được cài đặt trên máy tính. Thông thường, biểu tượng của SPSS sẽ được hiển thị trên màn hình chính hoặc trong danh sách ứng dụng. Sau khi khởi động, bạn sẽ thấy giao diện chính với các menu và công cụ.
Khởi động phần mềm là bước đầu tiên, nhưng không kém phần quan trọng. Khi giao diện xuất hiện, bạn sẽ thấy các tùy chọn như “Data View” và “Variable View”. “Data View” cho phép bạn nhập dữ liệu, trong khi “Variable View” giúp bạn định nghĩa các biến số mà bạn muốn phân tích.
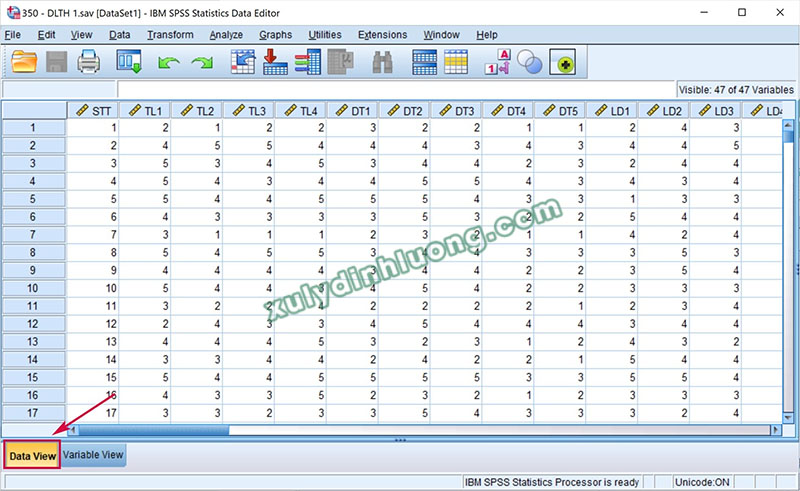
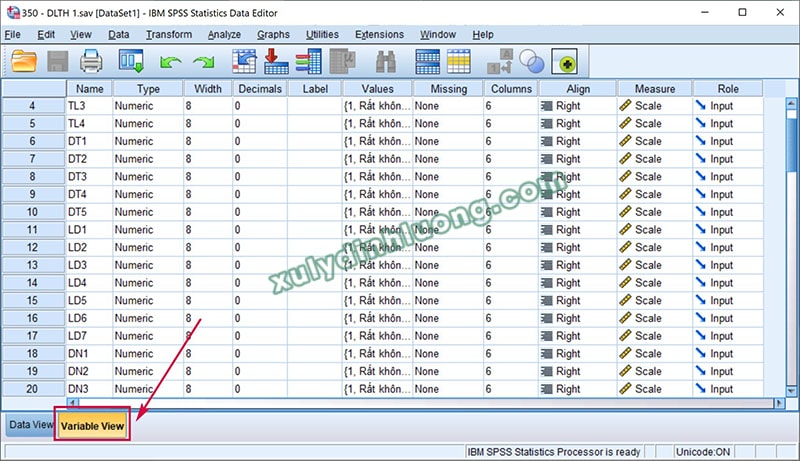
1.2 Nhập dữ liệu vào SPSS
Sau khi đã làm quen với giao diện, bước tiếp theo là nhập dữ liệu. Bạn có hai cách để nhập dữ liệu vào SPSS: nhập tay trực tiếp hoặc import từ file Excel hoặc CSV.
Nếu bạn nhập tay, hãy chắc chắn rằng bạn đã thiết lập đúng cấu trúc của bảng dữ liệu, với từng cột là một biến và mỗi hàng là một trường hợp. Nếu bạn sử dụng file Excel hay CSV, hãy chọn “File” -> “Open” để tải dữ liệu từ máy tính của bạn. Việc đầu tiên, chúng ta cần đảm bảo dữ liệu trình bày trong tệp Excel phải tuân theo tiêu chuẩn nhận diện của SPSS. Cấu trúc trình bày chuẩn SPSS của dữ liệu trên tập tin Excel như sau.
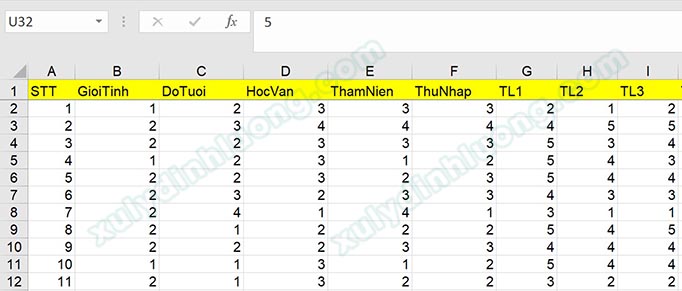
Hàng đầu tiên trong sheet Excel là tên biến, mỗi biến sẽ nằm ở một cột. Mỗi hàng tiếp theo trở đi tương ứng với câu trả lời của một đáp viên tham gia khảo sát. Cấu trúc này tương tự cách bố trí dữ liệu ở giao diện Data View trên SPSS.
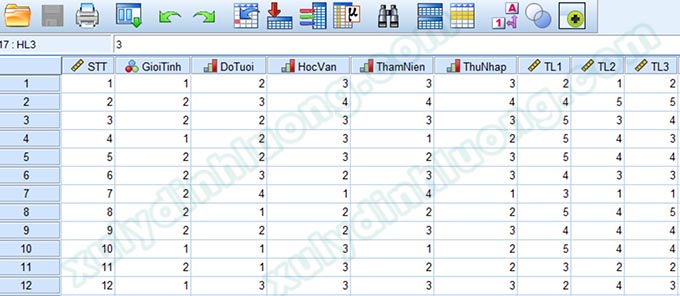
Để nhập dữ liệu từ tập tin Excel vào SPSS, trên giao diện SPSS 26, chúng ta vào File > Import Data > Excel…
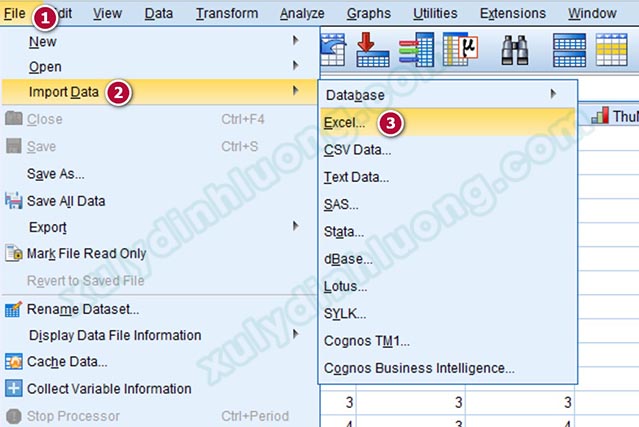
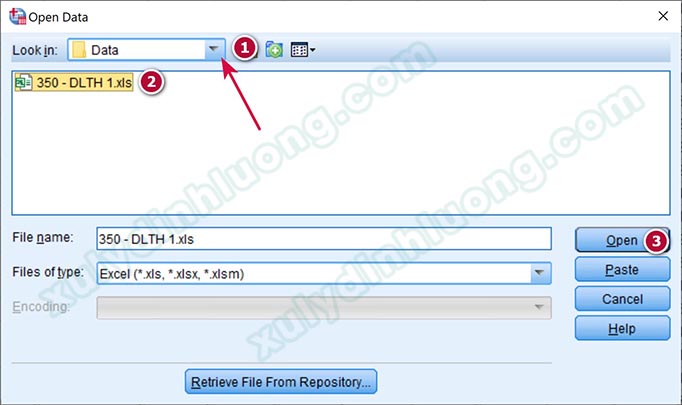
Cửa sổ Open Data xuất hiện, chúng ta nhấp vào nút tam giác ngược để dẫn đến thư mục chứa tệp dữ liệu Excel. Chọn tệp Excel cần mở, sau đó nhấp vào Open.
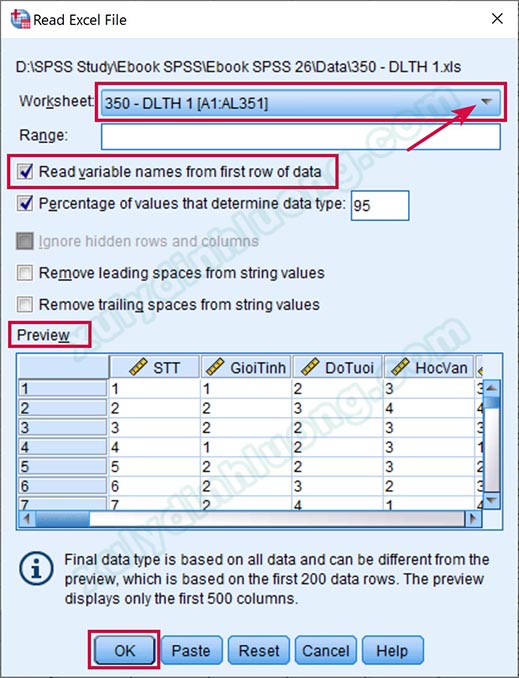
Trong cửa số tiếp theo, ở mục Worksheet, SPSS sẽ tự nhận diện dữ liệu cần nhập vào thuộc sheet đầu tiên của tệp Excel. Nếu dữ liệu chứa ở các sheet khác, chúng ta sẽ nhấp vào biểu tượng tam giác ngược để chọn sheet phù hợp. Tích chọn vào Read variable names from first row of data. Lựa chọn này cho phép phần mềm nhận hàng đầu tiên trong tệp Excel làm tên biến trong SPSS. Chúng ta có thể xem trước giao diện Variable View sau khi dữ liệu được nhập vào SPSS ở mục Preview. Nhấp vào OK để hoàn thành.
Lúc này chúng ta có thể hoàn toàn thao tác bình thường như một tập dữ liệu SPSS. Chúng ta nên lưu tập dữ liệu vừa được nhập từ Excel vào dưới định dạng .sav của SPSS và làm việc trực tiếp trên tập này để tránh các xung đột hay các vấn đề khác biệt về định dạng của hai phần mềm. Nếu về sau cần sử dụng tập dữ liệu dạng Excel, chúng ta sẽ xuất dữ liệu từ SPSS thành tập tin Excel bằng cách vào File > Export > Excel…
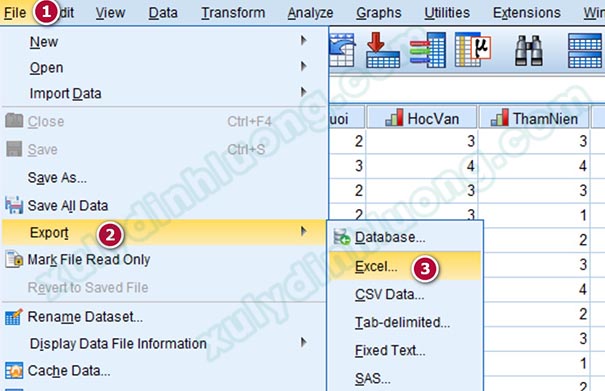
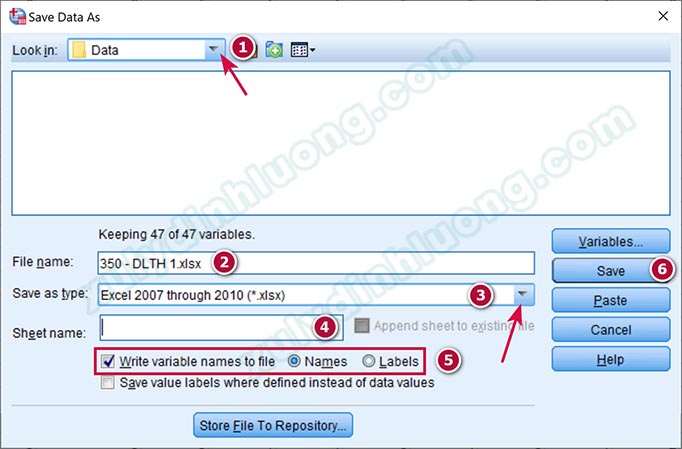
Trong cửa sổ xuất hiện, nhấp vào tam giác ngược mục Look in để chọn vị trí lưu tệp. Nhập tên tệp vào File name, chọn định dạng Excel muốn lưu tại Save as type, có thể nhập hoặc không nhập mục Sheet name. Trong mục Write variable names to file, chọn xuất tên biến là Name (tên biến trên SPSS) hoặc Labels (nhãn biến trên SPSS). Sau đó nhấp vào Save để tiến hành lưu tập tin.
Dữ liệu của bạn cần phải được tổ chức một cách hợp lý để đảm bảo quá trình phân tích diễn ra suôn sẻ. Mỗi biến cần phải có tên riêng và kiểu dữ liệu thích hợp, ví dụ như số nguyên, số thực, chuỗi văn bản,…
1.3 Định nghĩa các biến số
Trước khi chạy phân tích dữ liệu SPSS, chúng ta cần phải khai báo biến số cho dữ liệu trước. Việc định nghĩa các biến số là rất quan trọng vì nó ảnh hưởng đến cách bạn phân tích dữ liệu sau này. Trong tab “Variable View”, bạn có thể thay đổi các thuộc tính như tên biến, loại dữ liệu, độ dài, và nhãn cho biến. Điều này sẽ giúp bạn quản lý các biến một cách hiệu quả hơn.
Tùy dạng câu hỏi mà chúng ta sẽ có cách thức mã hóa tương ứng. Bạn vui lòng xem hai bài viết ở đây để hiểu rõ phương thức thực hiện cho mỗi dạng câu hỏi:
Mã hóa, nhập liệu câu hỏi khảo sát vào SPSS – Phần 1
Mã hóa, nhập liệu câu hỏi khảo sát vào SPSS – Phần 2
2. Hướng dẫn cách chạy SPSS toàn tập
Việc nắm vững cách chạy SPSS là điều cần thiết, đặc biệt đối với những người mới bắt đầu. SPSS cung cấp nhiều phương thức phân tích khác nhau, từ thống kê mô tả đến hồi quy và phân tích phương sai. Dưới đây là hướng dẫn mà bạn có thể tham khảo.
2.1 Thống kê mô tả
Bước đầu tiên trong các bước chạy SPSS, chúng ta sẽ thực hiện thống kê tần số cho các câu hỏi thông tin đáp viên như giới tính, độ tuổi để mô tả đặc điểm mẫu nghiên cứu của đề tài. Bảng tần số (Frequency) cung cấp cho chúng ta các thống kê về số lần xuất hiện giá trị, tỷ lệ cơ cấu phần trăm của giá trị,… Một số trường hợp biến định lượng mang giá trị tự do, bảng thống kê tần số sẽ rất dài do có quá nhiều giá trị, khi đó chúng ta sẽ mã hóa lại biến này rồi mới thực hiện thống kê tần số.
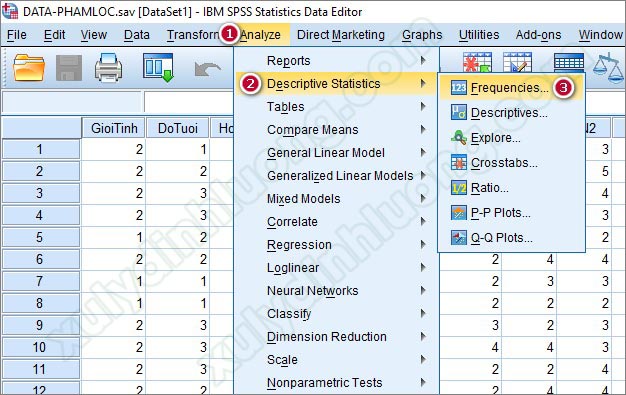
Cách chạy SPSS cho thống kê tần số: Từ giao diện cửa sổ SPSS, vào thẻ Analyze > Descriptive Statistics > Frequencies…
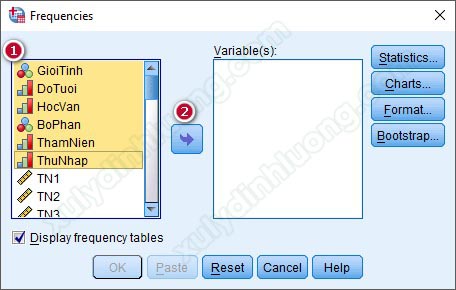
Tại cửa sổ hộp thoại Frequencies, đưa các biến cần thống kê tần số từ cột bên trái vào mục Variable(s) bên phải, có thể đưa cùng lúc nhiều biến vào thống kê tần số. Ở đây, chúng ta sẽ thực hiện thống kê tần số cho tất cả các biến thông tin cá nhân nên tác giả sẽ đưa tất cả các biến này vào mục Variable(s).
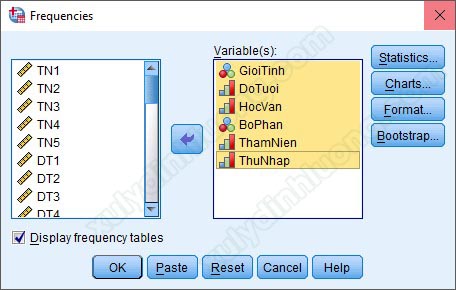
Sau khi đã đưa các biến cần thống kê tần số vào mục Variable(s), nhìn sang bên phải có các tùy chọn Statistics, Charts, Format và Bootstrap, đây là các mục để các bạn thống kê mô tả sâu hơn dữ liệu. Tuy nhiên, 2 mục được sử dụng nhiều nhất là Statistics và Charts. Đi vào tùy chọn Statistics:
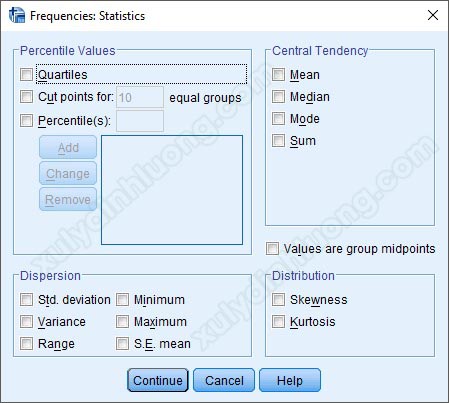
Có rất nhiều mục để bạn mô tả dữ liệu: Mean (trung bình), Median (trung vị), Mode (giá trị được chọn nhiều nhất), Sum (tổng), Minimum (giá trị nhỏ nhất), Maximum (giá trị lớn nhất), Std.deviation (độ lệch chuẩn)… Cần sử dụng mô tả nào, các bạn tích chọn vào mô tả đó, sau đó nhấp vào nút Continue. Tuy nhiên với dạng biến thông tin cá nhân như bảng khảo sát đang sử dụng, tác giả sẽ không tích chọn vào bất kỳ mục nào trong tùy chọn Statistics mà sẽ để mặc định.
Tiếp đến là tùy chọn Charts. Tùy chọn này cho phép SPSS xuất ra biểu đồ cho các biến đưa vào thống kê tần số.
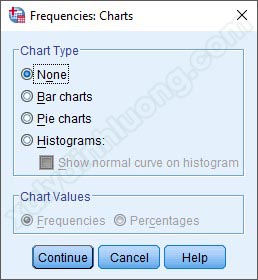
Các dạng biểu đồ được tích hợp trong tùy chọn Charts gồm: Bar charts (biểu đồ cột), Pie charts (biểu đồ tròn), Histograms (biểu đồ phân phối tần suất). Mục Chart Values bên dưới sẽ sáng lên và cho phép chọn dạng hiển thị tần số (Frequencies) hay phần trăm (Percentages) khi các bạn chọn 2 dạng biểu đồ Bar charts và Pie charts. Tuy nhiên, tác giả sẽ sử dụng mặc định là None ở mục này. Bởi vì thường với phần thống kê mô tả các biến thông tin cá nhân, chúng ta dùng 2 dạng biểu đồ chủ yếu là biểu đồ cột và biểu đồ tròn. Hai dạng biểu đồ này chắc hẳn các bạn đã được làm quen và thực hành vẽ trên công cụ Excel của bộ phần mềm văn phòng Microsoft Office. Tác giả nhận thấy vẽ biểu đồ trên Excel cho hình ảnh và màu sắc đẹp hơn, nhiều dạng biểu đồ hơn, tùy chọn linh hoạt hơn nên phần biểu đồ mô tả cơ cấu các biến cá nhân này, tác giả sẽ vẽ trên Excel chứ không sử dụng biểu đồ của SPSS.
Sau khi đã chọn dạng biểu đồ (tác giả không vẽ biểu đồ nên vẫn để tùy chọn mục này là None), các bạn nhấp vào nút Continue để quay lại giao diện ban đầu.
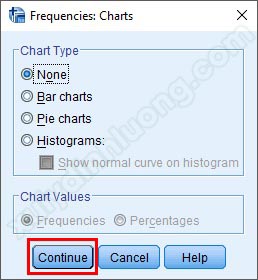
Tiếp tục nhấp vào OK, để xuất kết quả thống kê tần số ra Output.
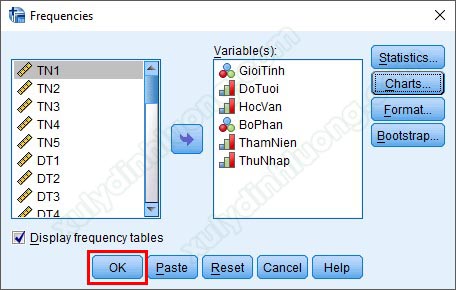
Kết quả từ Output, các bạn sẽ thấy 2 dạng bảng là Statistics thống kê chung tất cả các đã biến đưa vào và bảng Frequency thống tần số riêng lẻ cho từng biến.
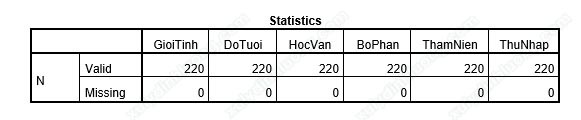
Trong bảng Statistics, các bạn sẽ thấy có 2 hàng là Valid và Missing. Valid cho biết số quan sát có giá trị hợp lệ (số người có trả lời). Missing cho biết số quan sát bị thiếu dữ liệu (số người không trả lời). Nếu trong bảng khảo sát, tất cả các câu hỏi đều không có trường hợp người dùng không chọn giá trị mà ở đây biến lại xuất hiện biến có Missing khác 0, các bạn cần kiểm tra lại phần Data View, xem lại mình có nhập thiếu dữ liệu hay không.
→ Thường bảng Statistics ít được dùng để trình bày vào bài nghiên cứu, bài luận. Bảng này được dùng nhiều vào việc làm sạch dữ liệu đã được giới thiệu ở chương 3.
Tiếp theo là bảng tần số của từng biến, mỗi biến đưa vào thực hiện thống kê tần số sẽ có một bảng riêng như ví dụ biến Độ tuổi dưới đây.
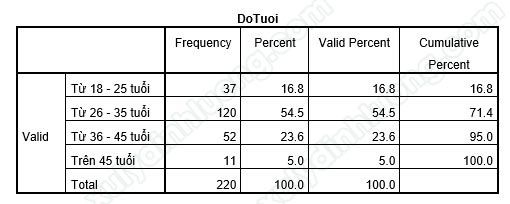
→ Trong tổng số 220 người tham gia trả lời phiếu khảo sát, có 37 người thuộc độ tuổi từ 18 đến 25 tuổi, 120 người thuộc độ tuổi từ 26 đến 35 tuổi, 52 người thuộc độ tuổi từ 36 đến 45 tuổi và có 11 người trên 45 tuổi.
→ Từ bảng thống kê, nhân viên trong công ty đa phần tập trung ở độ tuổi 26 đến 35 tuổi. Đây là độ tuổi lao động lý tưởng, có sự kết hợp giữa nhóm lao động trẻ giàu năng lượng cùng với nhóm lao động có khá nhiều kinh nghiệm làm việc.
Ý nghĩa các thông số của bảng:
- Frequency: Tần số (Có 37 người thuộc nhóm Từ 18 – 25 tuổi; có 120 người thuộc nhóm Từ 26 – 35 tuổi,…).
- Percent: Tỷ lệ phần trăm (Nhóm Từ 18 – 25 tuổi chiếm tỷ lệ 16.8%; nhóm Từ 26 – 35 tuổi chiếm tỷ lệ 54.5%,…).
- Valid Percent: Tỷ lệ phần trăm chỉ tính trên các giá trị hợp lệ. Nếu không có Missing, giá trị cột Valid Percent sẽ bằng với giá trị cột Percent.
- Cumulative Percent: Tỷ lệ phần trăm tích lũy chỉ tính trên các giá trị hợp lệ. Tỷ lệ phần trăm sẽ cộng dồn tới khi đủ 100% (Nhóm Từ 18 – 25 tuổi chiếm tỷ lệ 16.8%; nhóm Từ 18 – 25 tuổi và Từ 26 – 35 tuổi chiếm tổng tỷ lệ 71.4%,…).
Sau thống kê tần số, chúng ta sẽ đi vào thống kê trung bình để đánh giá mức điểm trả lời của đáp viên trên thang điểm khảo sát là cao hay thấp.
Thực hành phân tích thống kê trung bình trên SPSS với tập dữ liệu mẫu ở ví dụ ho nhóm Lương thưởng phúc lợi dưới đây:
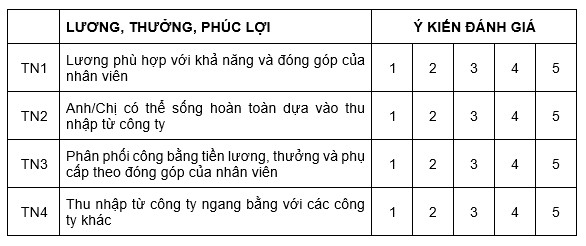
Chúng ta sẽ thực hiện thống kê mô tả cho các nhóm biến định lượng Likert. Việc sử dụng bảng mô tả cho các biến định lượng Likert nhằm so sánh giá trị trung bình Mean của các biến quan sát trong cùng 1 nhóm, xem biến nào đang được người được khảo sát đồng ý nhất, biến nào ít được đồng ý nhất,…từ đó giúp ích khá nhiều vào phần đề xuất, giải pháp cuối bài nghiên cứu.
Cách chạy SPSS cho thống kê trung bình: Chúng ta vào Analyze > Descriptive Statistics > Descriptives…
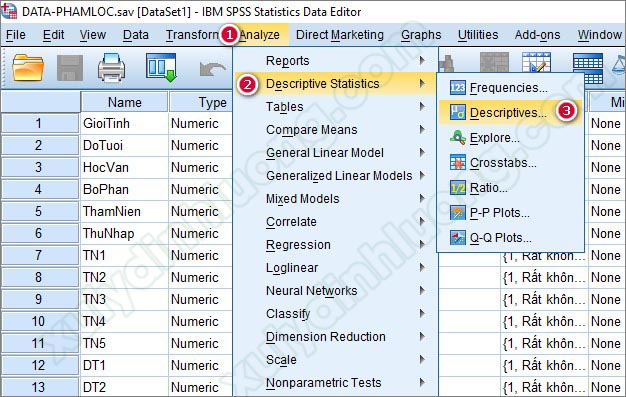
Tại cửa sổ hộp thoại Descriptives, đưa các biến cần thống kê mô tả từ cột bên trái vào mục Variable(s) bên phải, có thể đưa cùng lúc nhiều biến vào thực hiện thống kê. Dưới đây, chúng ta sẽ thực hiện thống kê mô tả cho nhóm biến Lương, thưởng, phúc lợi (từ TN1 đến TN5) nên tác giả sẽ đưa các biến này vào mục Variable(s).
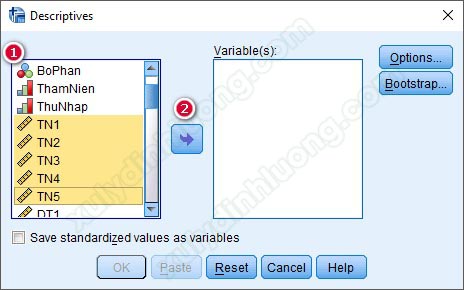
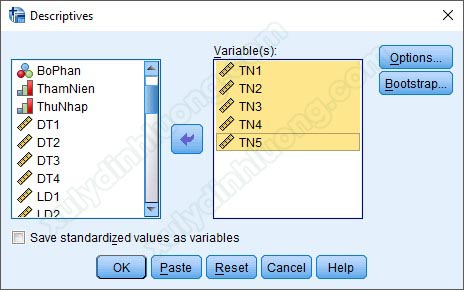
Sau khi đã đưa các biến cần thống kê tần số vào mục Variable(s), nhìn sang bên phải có các tùy chọn Options và Bootstrap, đây là các mục để các bạn mô tả sâu hơn dữ liệu. Tuy nhiên, thường chúng ta chỉ sử dụng đến mục Options.
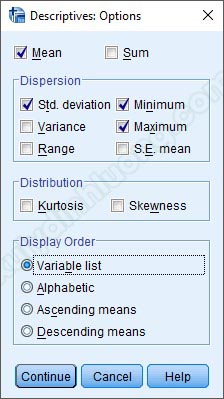
Trong Options, có các tùy chọn để chúng ta cho xuất hiện trong bảng mô tả, SPSS thiết lập mặc định các mục trong phần này gồm:
- Mean: giá trị trung bình.
- Deviation: độ lệch chuẩn.
- Minimum: giá trị nhỏ nhất
- Maximum: giá trị lớn nhất.
Tác giả không tích vào tùy chọn nào thêm mà chỉ sử dụng mặc định SPSS đề xuất. Nhấp chuột vào Continue để quay lại cửa sổ Descriptives, sau đó nhấp vào OK để xuất kết quả ra Output.
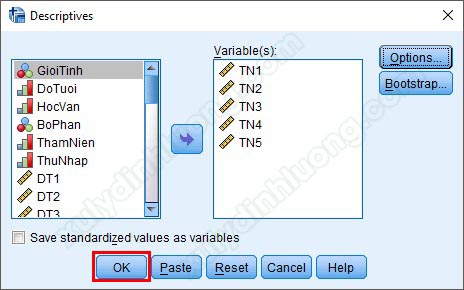
Tại cửa sổ Output, chúng ta sẽ quan tâm đến bảng Descriptive Statistics chứa các thông tin mô tả biến đưa vào.
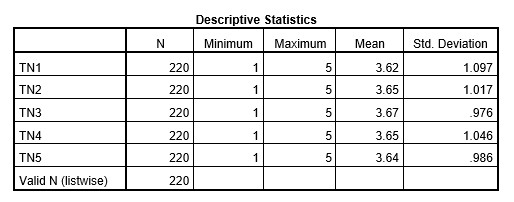
→ Giá trị trung bình của các biến quan sát từ TN1 đến TN5 trong nhóm Lương, thưởng, phúc lợi đều nằm trong mức điểm từ 3 đến 4 trên thang đo Likert 5 điểm. Như vậy, phần lớn các đáp viên tham gia trả lời bảng khảo sát đều đồng ý với các tiêu chí trong nhóm Lương, thưởng, phúc lợi.
→ Giá trị trung bình của TN1 cho đến TN5 không chênh lệch nhau nhiều và đều nằm trong mức điểm từ 3 đến 4 trên thang đo 5 điểm. Điều này cho thấy rằng công ty đang có chế độ đãi ngộ nhân viên khá tốt trên hầu hết các yếu tố: mức lương, thưởng, các chính sách về phúc lợi.
2.3 Phân tích độ tin cậy Cronbach’s Alpha
Phân tích Cronbach’s Alpha là một kỹ thuật thống kê được sử dụng rộng rãi trong nghiên cứu để đánh giá độ tin cậy nội bộ của một thang đo. Nói cách khác, nó giúp chúng ta trả lời câu hỏi: Các câu hỏi trong thang đo của tôi có thực sự đo lường cùng một khái niệm không? Một thang đo đảm bảo độ tin cậy tốt khi hệ số Cronbach’s Alpha từ 0.7 trở lên và không có biến quan sát có hệ số tương quan biến-tổng nhỏ hơn 0.3.
– Nếu một biến quan sát có hệ số tương quan biến tổng Corrected Item – Total Correlation ≥ 0.3 thì biến đó đạt yêu cầu. Hệ số Corrected Item – Total Correlation biểu thị mối tương quan giữa biến quan sát đó với các biến còn lại trong thang đo, nếu biến quan sát này có sự tương càng mạnh với các biến trong nhóm, biến đó càng tốt. Như vậy, khi thực hiện kiểm đinh độ tin cậy Cronbach’s Alpha, biến quan sát có hệ số tương quan biến tổng nhỏ hơn 0.3, cần loại biến đó và chạy lại lần 2.
– Mức giá trị hệ số Cronbach’s Alpha:
- Từ 0.8 đến gần bằng 1: thang đo lường rất tốt.
- Từ 0.7 đến gần bằng 0.8: thang đo lường sử dụng tốt.
- Từ 0.6 trở lên: thang đo lường đủ điều kiện.[4]
Chúng ta sẽ tới hướng dẫn cách chạy SPSS phần Cronbach’s Alpha trên SPSS để dễ hình dung hơn về thao tác. Để thực hiện kiểm định độ tin cậy thang đo Cronbach’s Alpha trong SPSS, chúng ta vào Analyze > Scale > Reliability Analysis…
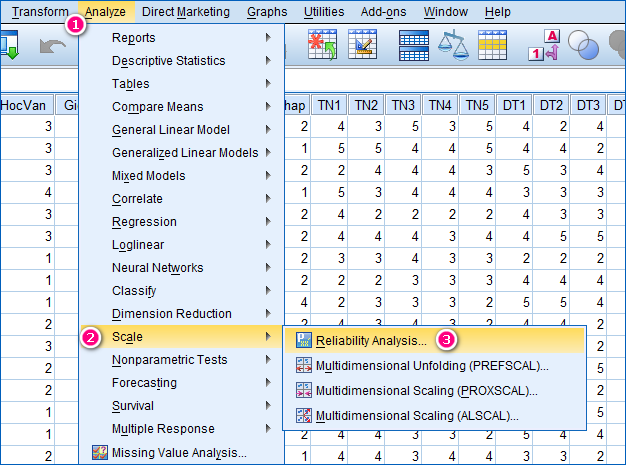
Thực hiện kiểm định cho nhóm biến quan sát thuộc nhân tố Lương, thưởng, phúc lợi (TN). Đưa 5 biến quan sát thuộc nhân tố TN vào mục Items bên phải. Tiếp theo chọn vào Statistics…
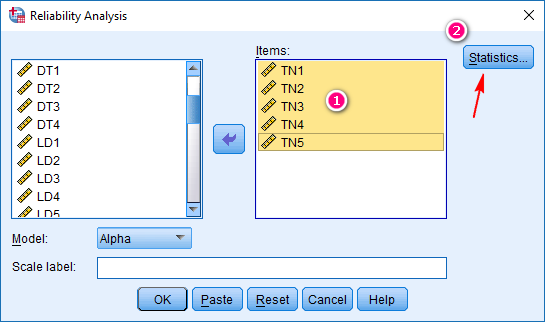
Trong tùy chọn Statistics, chúng ta tích vào các mục giống như hình. Sau đó chọn Continue để cài đặt được áp dụng.
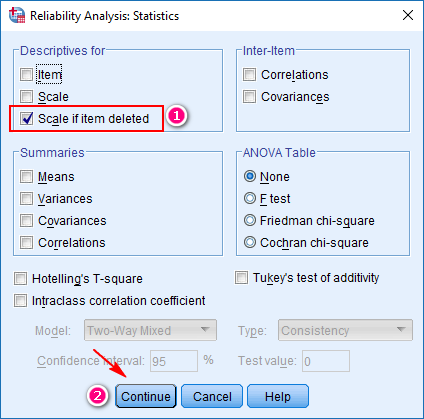
Sau khi click Continue, SPSS sẽ quay về giao diện ban đầu, chúng ta nhấp chuột vào OK để xuất kết quả ra Ouput:
Kết quả kiểm định độ tin cậy thang đo Cronbach’s Alpha của nhóm biến quan sát TN như sau:
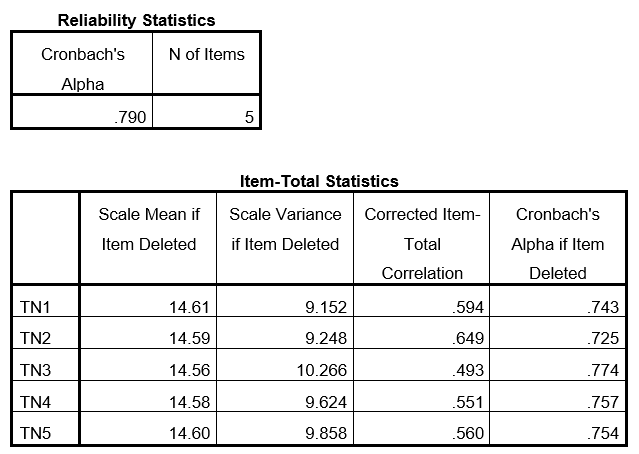
Kết quả kiểm định cho thấy các biến quan sát đều có hệ số tương quan tổng biến phù hợp (≥ 0.3). Hệ số Cronbach’s Alpha = 0.790 ≥ 0.6 nên đạt yêu cầu về độ tin cậy.
Chú thích các khái niệm:
- Cronbach’s Alpha: Hệ số Cronbach’s Alpha
- N of Items: Số lượng biến quan sát
- Scale Mean if Item Deleted: Trung bình thang đo nếu loại biến
- Scale Variance if Item Deleted: Phương sai thang đo nếu loại biến
- Corrected Item-Total Correlation: Tương quan biến tổng
- Cronbach’s Alpha if Item Deleted: Hệ số Cronbach’s Alpha nếu loại biến
2.3 Phân tích nhân tố khám phá EFA
Sau khi thực hiện xong Cronbach’ Alpha, chúng ta xác định các biến quan sát và các nhân tố đủ độ tin cậy để đưa vào phân tích nhân tố EFA. Lưu ý rằng, các biến quan sát kém chất lượng, các thang đo không đủ độ tin cậy bị loại ở bước Cronbach’s Alpha sẽ không được sử dụng lại ở bước EFA này.
Kiểm định độ tin cậy thang đo Cronbach’s Alpha tập trung đánh giá mức độ liên hệ giữa các biến trong cùng một nhóm hoặc cùng một nhân tố, mà không xem xét mối quan hệ giữa các biến quan sát thuộc các nhân tố khác. Ngược lại, phân tích nhân tố khám phá (EFA) xem xét mối quan hệ giữa các biến trên tất cả các nhóm (nhân tố) khác nhau, nhằm phát hiện những biến quan sát có tải trọng lên nhiều nhân tố hoặc bị phân bổ sai nhân tố so với dự kiến ban đầu.
Các tiêu chí đánh giá trong EFA:
– Hệ số KMO (Kaiser-Meyer-Olkin) là một chỉ số dùng để xem xét sự thích hợp của phân tích nhân tố. Trị số của KMO phải đạt giá trị 0.5 trở lên (0.5 ≤ KMO ≤ 1) là điều kiện đủ để phân tích nhân tố là phù hợp.
– Kiểm định Bartlett (Bartlett’s test of sphericity) là một kiểm định xem xét có mối tương quan xảy ra giữa các biến tham gia vào EFA. Giả định rất quan trọng trong EFA là các biến quan sát đưa vào phân tích cần có sự tương quan với nhau. Thay vì đánh giá dựa vào ma trận tương quan khá khó khăn, chúng ta sẽ dùng tới kiểm định Bartlett, nếu sig kiểm định Bartlett nhỏ hơn 0.05, chúng ta kết luận các biến tham gia vào EFA có sự tương quan với nhau, phân tích EFA là phù hợp
– Tổng phương sai trích (Total Variance Explained) ≥ 50% cho thấy mô hình EFA là phù hợp. Coi biến thiên là 100% thì trị số này thể hiện các nhân tố được trích cô đọng được bao nhiêu % và bị thất thoát bao nhiêu % của các biến quan sát.
– Hệ số tải nhân tố (Factor Loading) hay còn gọi là trọng số nhân tố, giá trị này biểu thị mối quan hệ tương quan giữa biến quan sát với nhân tố. Hệ số tải nhân tố càng cao, nghĩa là tương quan giữa biến quan sát đó với nhân tố càng lớn và ngược lại. Theo Hair & ctg (2009,116), Multivariate Data Analysis, 7th Edition thì:
- Factor Loading ở mức ± 0.3: Điều kiện tối thiểu để biến quan sát được giữ lại.
- Factor Loading ở mức ± 0.5: Biến quan sát có ý nghĩa thống kê tốt (mức sử dụng phổ biến).
- Factor Loading ở mức ± 0.7: Biến quan sát có ý nghĩa thống kê rất tốt.
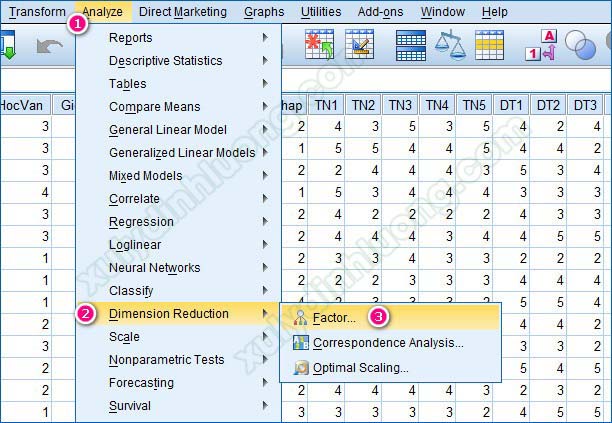
Cách chạy SPSS phần phân tích EFA: Để thực hiện phân tích nhân tố khám phá EFA trong SPSS, chúng ta vào Analyze > Dimension Reduction > Factor…
Đưa các biến quan sát cần thực hiện phân tích EFA vào mục Variables. Chú ý 4 tùy chọn được đánh số ở ảnh bên dưới.
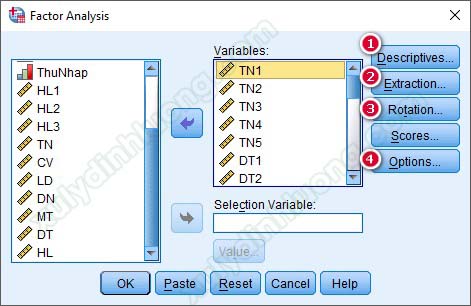
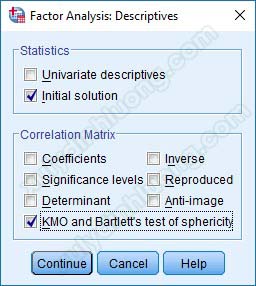
– Descriptives: Tích vào mục KMO and Barlett’s test of sphericity để xuất bảng giá trị KMO và giá trị sig của kiểm định Barlett. Nhấp Continue để quay lại cửa sổ ban đầu.
– Extraction: Ở đây, chúng ta sẽ sử dụng phép trích PCA (Principal Components Analysis). Với SPSS 20 và các phiên bản 21, 22, 23, 24, PCA sẽ được viết gọn lại là Principal Components như hình ảnh bên dưới, đây cũng là tùy chọn mặc định của SPSS.
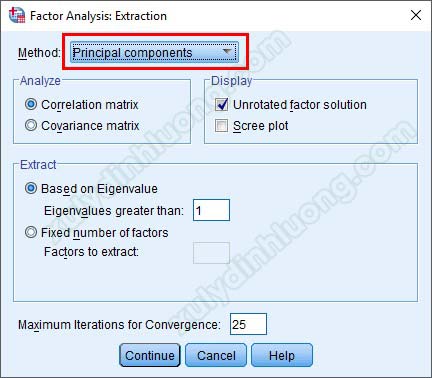
Khi các bạn nhấp chuột vào nút mũi tên hướng xuống sẽ có nhiều tùy chọn phép trích khác nhau. Số lượng nhân tố được trích ra ở ma trận xoay phụ thuộc khá nhiều vào việc lựa chọn phép trích, tuy nhiên, tài liệu này sẽ chỉ tập trung vào phần PCA.
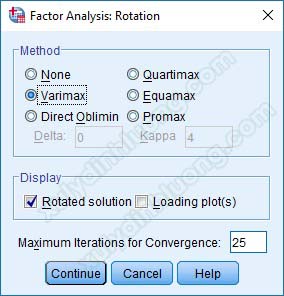
– Rotation: Ở đây có các phép quay, thường chúng ta hay sử dụng Varimax và Promax. Riêng với dạng đề tài đã xác định được biến độc lập và biến phụ thuộc, chúng ta sử dụng phép quay Varimax. Nhấp Continue để quay lại cửa sổ ban đầu.
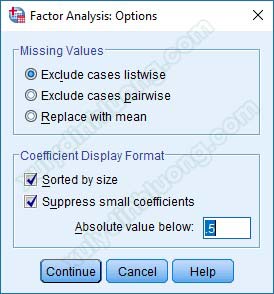
– Options: Tích vào 2 mục như hình bên dưới. Sorted by size giúp sắp xếp ma trận xoay thành từng cột dạng bậc thang để dễ đọc dữ liệu hơn. Suppress small coefficients giúp loại bỏ các hệ số tải không đạt tiêu chuẩn khỏi ma trận xoay, giúp ma trận gọn gàng, trực quan hơn. Tại mục này sẽ có hàng Absolute value below, bạn cần nhập vào giá trị hệ số tải nhân tố Factor Loading tiêu chuẩn. Kích thước mẫu file dữ liệu là 220 nên tác giả sẽ nhập vào 0.5. Nhấp Continue để quay lại cửa sổ ban đầu.
Tại cửa sổ tiếp theo, bạn chọn OK để xuất kết quả ra Output.
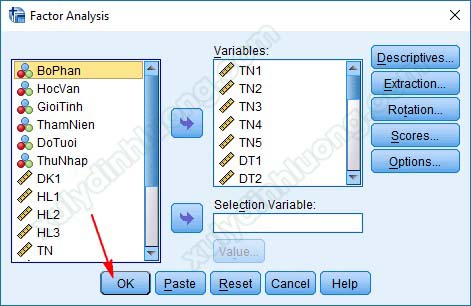
Có khá nhiều bảng ở Ouput, tuy nhiên, chúng ta chỉ cần quan tâm 3 bảng:
- KMO and Barlett’s Test:xem hệ số KMO và sig kiểm định Bartlett.
- Total Variance Explained:xem tổng phương sai trích Total Variance Explained và giá trị Eigenvalue.
- Rotated Component Matrix: xem ma trận xoay và kiểm tra hệ số tải Factor Loading của các biến quan sát (Lưu ý tránh nhầm lẫn với bảng Component Matrix)
Không phải lúc nào ma trận xoay có được từ kết quả phân tích EFA cũng tách biệt các nhóm một cách hoàn toàn, việc xuất hiện các biến xấu sẽ làm ma trận xoay bị xáo trộn so với các thang đo lý thuyết. Vậy cách khắc phục ma trận xoay lộn xộn như thế nào, bạn hãy xem tại bài viết này.
2.4 Phân tích tương quan Pearson
Sau bước EFA, chúng ta đã xác định được các nhân tố phù hợp được hình thành. Tiếp theo chúng ta sẽ tạo biến đại diện cho các nhân tố này để sử dụng cho phần phân tích tương quan + hồi quy. Nếu bạn chưa rõ về cách tạo biến đại diện, vui lòng xem tại bài viết Tạo nhân tố, biến đại diện sau phân tích EFA.
Sau khi đã có được biến đại diện, chúng ta phân tích tương quan tuyến tính Pearson để đánh giá mối quan hệ giữa các biến trong mô hình.
Việc đánh giá mối quan hệ tương quan giữa hai biến không chỉ duy nhất dựa vào các con số, bởi có khả năng xảy ra tình trạng tương quan giả. Hai biến định lượng có hệ số tương quan rất cao nhưng thực tế lại không có mối quan hệ nào cả. Việc xuất hiện tương quan cao giữa hai biến không có mối quan hệ đến từ sự ngẫu nhiên trong xu hướng dữ liệu của mẫu hoặc một kết quả tình cờ từ một nguyên nhân chung nào đó. Ví dụ, kết quả tương quan Pearson cho thấy thu nhập trung bình đầu người tại Việt Nam và số lượng thiên tai qua các năm có sự tương quan thuận với nhau, chúng ta có thể đánh giá rằng đây là một kết quả tình cờ.
Mối liên hệ tương quan tuyến tính khác với liên hệ nhân quả. Để đánh giá sự tương quan tuyến tính giữa một cặp biến, chúng ta dùng phân tích tương quan Pearson. Nhưng để đánh giá mối liên hệ nhân quả, biến A thay đổi gây ra kết quả gì cho biến B, chúng ta cần sử dụng đến hồi quy. Nên nhớ rằng, không phải lúc nào hai biến có mối quan hệ tương quan thì giữa chúng cũng có mối liên hệ nhân quả với nhau. Ví dụ, lợi nhuận kinh doanh có sự tương quan chặt chẽ với số chi nhánh của nhà hàng, nhưng việc tăng số chi nhánh không phải lúc nào cũng làm tăng cao lợi nhuận. Lợi nhuận tăng sau khi nhà hàng mở thêm chi nhánh có thể là do sự tăng lên số lượng chi nhánh mới nhưng cũng có thể là do hiệu quả từ chiến dịch marketing rầm rộ, do sự tối ưu chi phí đầu vào… Thậm chí, việc tăng số chi nhánh còn chẳng tác động gì đến lợi nhuận, hoặc mức độ tác động đến lợi nhuận không lớn như hệ số tương quan r thể hiện.
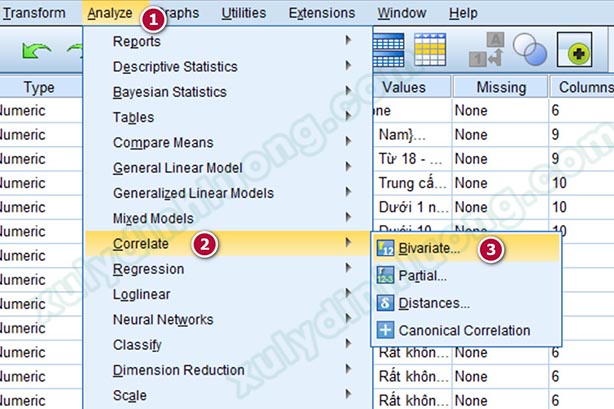
Đi vào hướng dẫn cách chạy SPSS phần tương quan Pearson, tại giao diện SPSS, các bạn vào Analyze > Correlate > Bivariate…
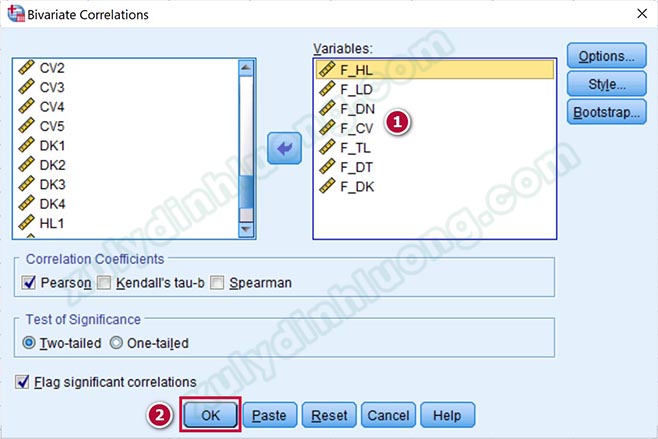
Tại đây, chúng ta đưa hết tất cả các biến muốn chạy tương quan Pearson vào mục Variables, cụ thể là các biến đại diện được tạo ra sau bước phân tích EFA. Để tiện cho việc đọc kết quả, chúng ta nên đưa biến phụ thuộc lên trên cùng. Nhấp vào OK để xác nhận thực hiện lệnh.
Kết quả tương quan Pearson sẽ được thể hiện trong bảng Correlations. Điểm qua các ký hiệu trong bảng này: Pearson Correlation là hệ số tương quan Pearson (r), Sig. (2-tailed) là giá trị sig của kiểm định t đánh giá hệ số tương quan Pearson có ý nghĩa thống kê hay không, N là cỡ mẫu.
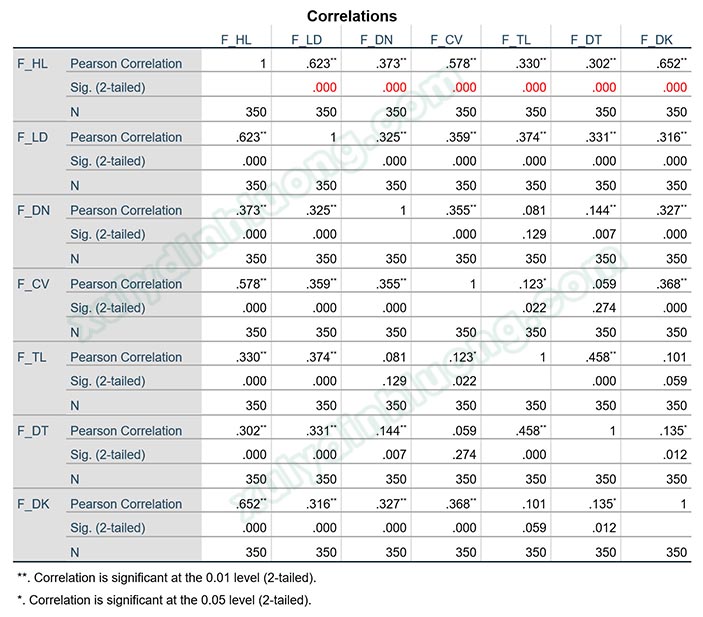
Chúng ta sẽ xem xét hai loại mối quan hệ tương quan: tương quan giữa biến phụ thuộc với các biến độc lập và tương quan giữa các biến độc lập với nhau. Sở dĩ việc chia ra như vậy, vì sự kỳ vọng về kết quả sẽ có đôi chút khác biệt giữa hai loại mối quan hệ này. Với sự tương quan giữa các biến độc lập với biến phụ thuộc, khi xây dựng mô hình nghiên cứu chúng ta đã tìm hiểu rất kỹ để tìm ra các biến độc lập có sự tác động lên biến phụ thuộc. Việc đưa ra các biến độc lập này dựa trên nền tảng cơ sở lý thuyết, các nghiên cứu tương tự trước đó và sự đánh giá tình hình thực tế tại môi trường khảo sát. Do đó, chúng ta kỳ vọng rằng kết quả phân tích từ dữ liệu sẽ cho thấy các biến độc lập có sự tương quan với biến phụ thuộc hoặc có sự tác động lên biến phụ thuộc. Nếu chúng ta thực hiện phân tích tương quan trước hồi quy, kết quả từ tương quan Pearson cho thấy biến độc lập có tương quan với biến phụ thuộc, khả năng biến độc lập đó sẽ tác động lên biến phụ thuộc ở hồi quy sẽ cao hơn.
Loại quan hệ thứ hai là tương quan giữa các biến độc lập với nhau. Tên gọi “biến độc lập” phần nào nói lên được đặc điểm kỳ vọng của dạng biến này: chúng độc lập về ý nghĩa với nhau. Giữa hai biến độc lập nếu có sự tương quan quá mạnh, có khả năng hai biến này bản chất chỉ là một biến, một khái niệm. Nếu hai hay nhiều biến độc lập tương quan mạnh với nhau cùng tham gia vào một phép hồi quy sẽ dễ dẫn đến hiện tượng cộng tuyến/đa cộng tuyến gây sai lệch kết quả thống kê. Do đó, chúng ta kỳ vọng rằng không có sự tương quan quá mạnh giữa các biến độc lập. Khi đồng thời sig kiểm định t của hai biến độc lập nhỏ hơn 0.05 và trị tuyệt đối hệ số tương quan Pearson giữa chúng lớn hơn 0.7, chúng ta cần hết sức lưu ý đến cặp biến này để đưa ra hướng xử lý trong trường hợp xảy ra tình trạng cộng tuyến/đa cộng tuyến.
Quay lại với kết quả tương quan Pearson từ ví dụ ở trên, sig kiểm định t tương quan Pearson các giữa sáu biến độc lập F_LD, F_DN, F_CV, F_TL, F_DT, F_DK với biến phụ thuộc F_HL đều nhỏ hơn 0.05. Như vậy, có mối liên hệ tuyến tính giữa các biến độc lập này với biến phụ thuộc. Giữa các biến độc lập, không có mối tương quan nào quá mạnh khi trị tuyệt đối hệ số tương quan giữa các cặp biến đều nhỏ hơn 0.5, như vậy khả năng xảy ra hiện tượng cộng tuyến/đa cộng tuyến cũng thấp hơn.
2.5 Phân tích hồi quy tuyến tính bội
Khác với tương quan Pearson, trong hồi quy đa biến các biến không có tính chất đối xứng như phân tích tương quan. Vai trò giữa biến độc lập và biến phụ thuộc là khác nhau. X và Y hay Y và X có tương quan với nhau đều mang cùng một ý nghĩa, trong khi đó với hồi quy, ta chỉ có thể nhận xét: X tác động lên Y hoặc Y chịu tác động bởi X.
Các tiêu chí trong phân tích hồi quy:
a. Giá trị R2 (R Square), R2 hiệu chỉnh (Adjusted R Square)
Giá trị R2 và R2 hiệu chỉnh phản ánh mức độ giải thích biến phụ thuộc của các biến độc lập trong mô hình hồi quy. R2 hiệu chỉnh phản ánh sát hơn so với R2. Mức dao động của 2 giá trị này là từ 0 đến 1, tuy nhiên việc đạt được mức giá trị bằng 1 là gần như không tưởng dù mô hình đó tốt đến nhường nào. Giá trị này thường nằm trong bảng Model Summary. Cần chú ý, không có tiêu chuẩn chính xác R2 hiệu chỉnh ở mức bao nhiêu thì mô hình mới đạt yêu cầu, chỉ số này nếu càng tiến về 1 thì mô hình càng có ý nghĩa, càng tiến về 0 thì ý nghĩa mô hình càng yếu. Thường chúng ta chọn mức trung gian là 0.5 để phân ra 2 nhánh ý nghĩa mạnh/ý nghĩa yếu, từ 0.5 đến 1 thì mô hình là tốt, bé hơn 0.5 là mô hình chưa tốt. Tuy nhiên, tùy vào dạng nghiên cứu và dạng dữ liệu, không phải lúc nào cũng bắt buộc rằng mô hình hồi quy phải đạt giá trị R2 hiệu chỉnh lớn hơn 0.5 mới có ý nghĩa.
b. Kiểm định F
Giá trị sig của kiểm định F được sử dụng để kiểm định độ phù hợp của mô hình hồi quy. Nếu sig nhỏ hơn 0.05, ta kết luận mô hình hồi quy tuyến tính bội phù hợp với tập dữ liệu và có thể sử đụng được. Giá trị này thường nằm trong bảng ANOVA.
c. Kiểm định t
Giá trị sig của kiểm định t được sử dụng để kiểm định ý nghĩa của hệ số hồi quy. Nếu sig kiểm định t của hệ số hồi quy của một biến độc lập nhỏ hơn 0.05, ta kết luận biến độc lập đó có tác động đến biến phụ thuộc. Nếu sig kiểm định t của biến độc lập lớn hơn 0.05, chúng ta kết luận biến độc lập đó không có sự tác động lên biến phụ thuộc, và không cần loại bỏ biến đó để chạy lại hồi quy lần tiếp theo. Mỗi biến độc lập tương ứng với một hệ số hồi quy riêng, do vậy mà ta cũng có từng kiểm định t riêng. Giá trị này thường nằm trong bảng Coefficients.
d. Đa cộng tuyến VIF
Hệ số phóng đại phương sai VIF dùng để kiểm tra hiện tượng đa cộng tuyến. Thông thường, nếu VIF của một biến độc lập lớn hơn 10 nghĩa là đang có đa cộng tuyến xảy ra với biến độc lập đó. Khi đó, biến này sẽ không có giá trị giải thích biến thiên của biến phụ thuộc trong mô hình hồi quy. Với các đề tài sử dụng thang đo Likert, nếu hệ số VIF > 2 thì khả năng rất cao đang xảy ra hiện tượng đa cộng tuyến giữa các biến độc lập. Giá trị này thường nằm trong bảng Coefficients.
Cách chạy SPSS kết quả hồi quy tuyến tính:
Phần thực hành này tác giả có một tập data mẫu với biến phụ thuộc là Sự hài lòng của nhân viên (ký hiệu HL), các biến độc lập là:
- Lương, thưởng, phúc lợi: TN
- Bản chất công việc: CV
- Quan hệ với lãnh đạo: LD
- Môi trường làm việc: MT
- Đào tạo và thăng tiến: DT
Thực hiện phân tích hồi quy tuyến tính bội để đánh giá sự tác động của các biến độc lập này đến biến phụ thuộc HL. Để thực hiện phân tích hồi quy đa biến trong SPSS, chúng ta vào Analyze > Regression > Linear…
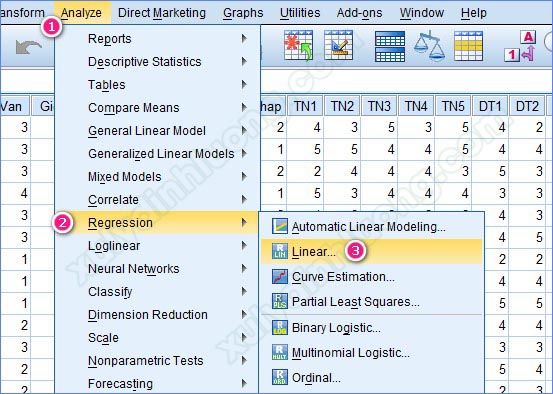
Đưa biến phụ thuộc vào ô Dependent, các biến độc lập vào ô Indenpendents:
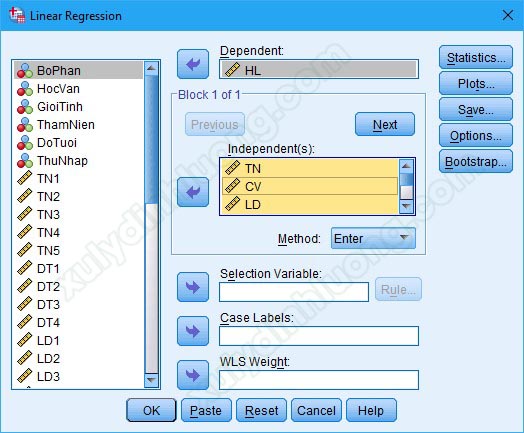
Vào mục Statistics, tích chọn các mục như trong ảnh và chọn Continue:
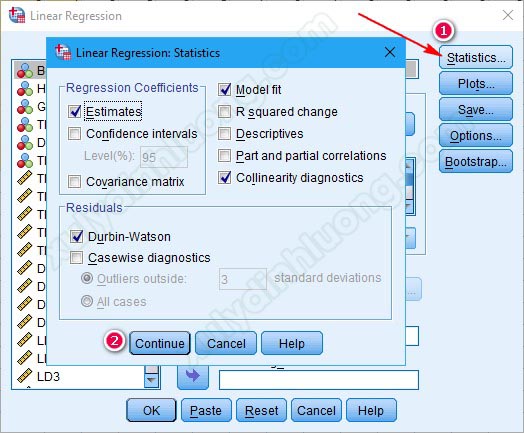
Các mục còn lại chúng ta sẽ để mặc định. Quay lại giao diện ban đầu, mục Method là các phương pháp chạy hồi quy, 2 method phổ biến nhất là Stepwise và Enter, thường thì sẽ chọn Enter. Chọn xong phương pháp, các bạn nhấp vào OK.
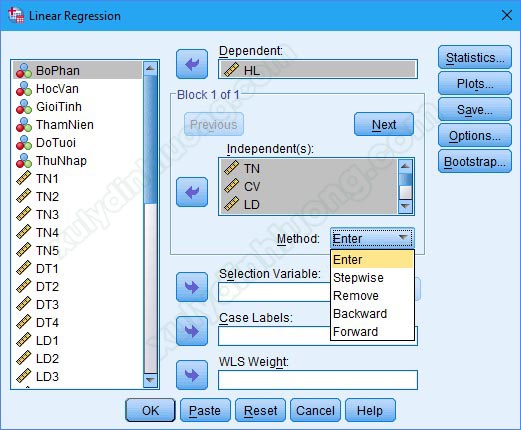
SPSS sẽ xuất ra rất nhiều bảng, những bảng các bạn cần sử dụng là: Model Summary, ANOVA, Coefficients.
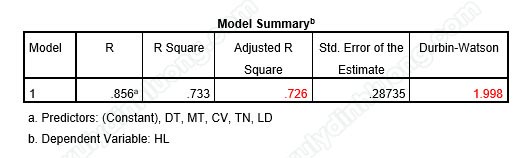
→ Giá trị R2 hiệu chỉnh bằng 0.726 cho thấy biến độc lập đưa vào chạy hồi quy ảnh hưởng 72.6% sự thay đổi của biến phụ thuộc, còn lại 27.4% là do các biến ngoài mô hình và sai số ngẫu nhiên.
→ Hệ số Durbin – Watson = 1.998, nằm trong khoảng 1.5 đến 2.5 nên không có hiện tượng tự tương quan chuỗi bậc nhất xảy ra.
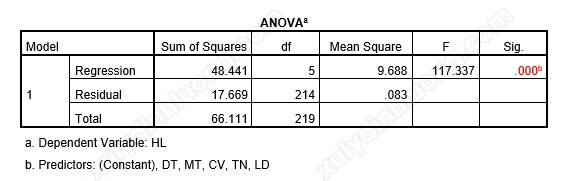
→ Sig kiểm định F bằng 0.00 < 0.05, như vậy, mô hình hồi quy tuyến tính bội phù hợp với tập dữ liệu và có thể sử đụng được.
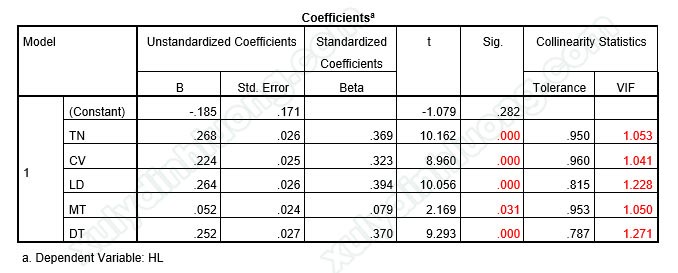
→ Sig kiểm định t hệ số hồi quy của các biến độc lập đều nhỏ hơn 0.05, do đó các biến độc lập đều có ý nghĩa giải thích cho biến phụ thuộc, không biến nào bị loại khỏi mô hình.
(Lưu ý rằng SPSS ký hiệu .031 nghĩa là 0.031. SPSS tự động loại bỏ số 0 trước dấu phẩy phần thập phân một số bảng kết quả như tương quan, hồi quy,…)
→ Hệ số VIF của các biến độc lập đều nhỏ hơn 10 do vậy không có đa cộng tuyến xảy ra.
→ Các hệ số hồi quy đều lớn hơn 0. Như vậy tất cả các biến độc lập đưa vào phân tích hồi quy đều tác động cùng chiều tới biến phụ thuộc. Dựa vào độ lớn của hệ số hồi quy chuẩn hóa Beta, thứ tự mức độ tác động từ mạnh nhất tới yếu nhất của các biến độc lập tới biến phụ thuộc HL là: LD (0.394) > DT(0.370) > TN (0.369) > CV (0.323) > MT (0.079). Tương ứng với:
- Biến Lãnh đạo và cấp trên tác động mạnh nhất tới sự hài lòng của nhân viên.
- Biến Cơ hội đào tạo và thăng tiến tác động mạnh thứ 2 tới sự hài lòng của nhân viên.
- Biến Lương, thưởng, phúc lợi tác động mạnh thứ 3 tới sự hài lòng của nhân viên.
- Biến Bản chất công việc tác động mạnh thứ 4 tới sự hài lòng của nhân viên.
- Biến Điều kiện làm việc tác động yếu nhất tới sự hài lòng của nhân viên.
Kết luận, với 6 giả thuyết từ H1 đến H6 chúng ta đã đặt ra ban đầu ở mục Giả thuyết nghiên cứu (mục 1.3). Có 5 giả thuyết được chấp nhận là: H1, H2, H3, H5, H6 tương ứng với các biến: Lãnh đạo và cấp trên; Cơ hội đào tạo và thăng tiến; Lương, thưởng, phúc lợi; Bản chất công việc; Điều kiện làm việc. Riêng giả thuyết H4 bị bác bỏ, yếu tố Đồng nghiệp không tác động đến Sự hài lòng của nhân viên trong công việc tại công ty TNHH Nhãn Xanh, hay nói cách khác, biến Đồng nghiệp không có ý nghĩa trong mô hình hồi quy.
Phương trình hồi quy chuẩn hóa:
HL = 0.394*LD + 0.370*DT + 0.369*TN + 0.323*CV + 0.079*MT + e
Sự hài lòng của nhân viên = 0.394 * Lãnh đạo và cấp trên
+ 0.370 * Cơ hội đào tạo và thăng tiến
+ 0.369 * Lương, thưởng, phúc lợi
+ 0.323 * Bản chất công việc
+ 0.079 * Điều kiện làm việc
3. Kết luận
Việc chạy SPSS không phải là một nhiệm vụ khó khăn nếu bạn nắm vững các bước cơ bản và thực hành thường xuyên. Bài viết này đã cung cấp cho bạn cái nhìn tổng quan về cách chạy SPSS, hướng dẫn cách chạy SPSS, và các phương pháp phân tích dữ liệu hiệu quả. Phạm vi một bài viết không thể truyền tải hết đầy đủ và trọn vẹn nội dung tất cả các phân tích trên SPSS nên các bạn có thể tham khảo Giáo trình hướng dẫn sử dụng SPSS toàn tập kèm dữ liệu thực hành để hỗ trợ cho việc học tập hiệu quả hơn nhé.
Hy vọng rằng những kiến thức và kinh nghiệm mà chúng tôi chia sẻ sẽ giúp bạn tự tin hơn khi làm việc với phần mềm SPSS, từ đó nâng cao khả năng phân tích và ra quyết định trong công việc của mình.










