Sau khi thực hiện phân tích hồi quy đa biến trên SPSS, chúng ta cần phải kiểm tra xem kết quả có bị vi phạm các giả định hồi quy hay không. Nếu các giả định bị vi phạm thì kết quả tính toán ra sẽ không đáng tin cậy nữa. Các giả định quan trọng gồm: phần dư phải có phân phối chuẩn, biến độc lập và phụ thuộc phải có liên hệ tuyến tính, phương sai phần dư không thay đổi.

1. Giả định: Phân phối chuẩn của phần dư
Giả định đầu tiên đó là phần dư trong hồi quy phải xấp xỉ phân phối chuẩn. Phần dư có thể không tuân theo phân phối chuẩn vì những lý do như: sử dụng sai mô hình, phương sai không phải là hằng số, số lượng các phần dư không đủ nhiều để phân tích… Vì vậy, chúng ta cần thực hiện nhiều cách khảo sát khác nhau. Hai cách phổ biến nhất là căn cứ vào biểu đồ Histogram và Normal P-P Plot phần dư.
Đối với biểu đồ Histogram, nếu giá trị trung bình Mean gần bằng 0, độ lệch chuẩn gần bằng 1, đường cong phân phối có dạng hình chuông ta có thể khẳng định phân phối là xấp xỉ chuẩn, giả định phân phối chuẩn của phần dư không bị vi phạm.
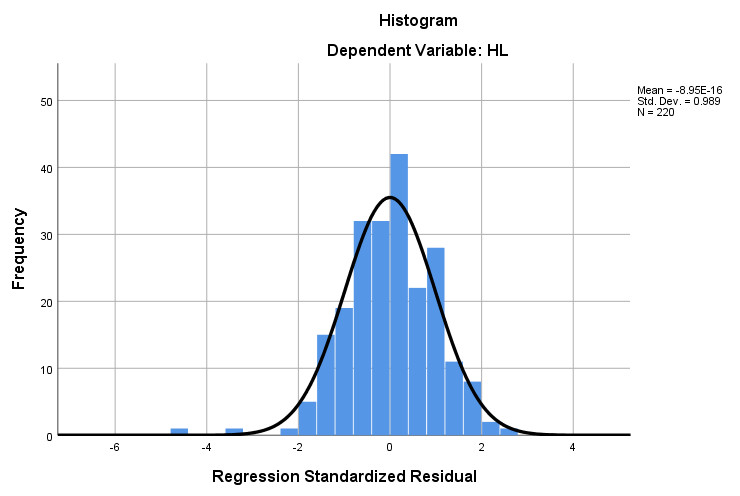
→ Cụ thể trong ví dụ này, giá trị trung bình Mean = -8.95E-16 gần bằng 0, độ lệch chuẩn là 0.989 gần bằng 1, như vậy có thể nói, phân phối phần dư xấp xỉ chuẩn. Do đó, có thể kết luận rằng, giả định phân phối chuẩn của phần dư không bị vi phạm.
Đối với biểu đồ Normal P-P Plot, nếu các điểm phân vị trong phân phối của phần dư tập trung thành 1 đường chéo như hình bên dưới, nghĩa là phần dư có phân phối chuẩn. Như vậy, giả định phân phối chuẩn của phần dư không bị vi phạm.
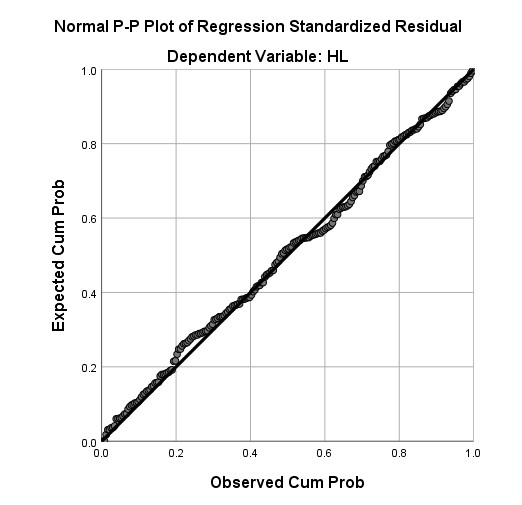
→ Các điểm phân vị trong phân phối của phần dư tập trung thành 1 đường chéo, như vậy, giả định phân phối chuẩn của phần dư không bị vi phạm.
2. Giả định: Liên hệ tuyến tính giữa biến phụ thuộc với biến độc lập
Giả định thứ hai đó là phải có mối liên hệ tuyến tính giữa biến phụ thuộc với các biến độc lập. Biểu đồ phân tán Scatter Plot giữa các phần dư chuẩn hóa và giá trị dự đoán chuẩn hóa giúp chúng ta dò tìm xem dữ liệu hiện tại có vi phạm giả định liên hệ tuyến tính hay không. Nếu phần dư chuẩn hóa phân bổ ngẫu nhiên xung quanh đường tung độ 0 và hình dạng tạo thành một đường thẳng, chúng ta có thể kết luận giả định quan hệ tuyến tính không bị vi phạm.
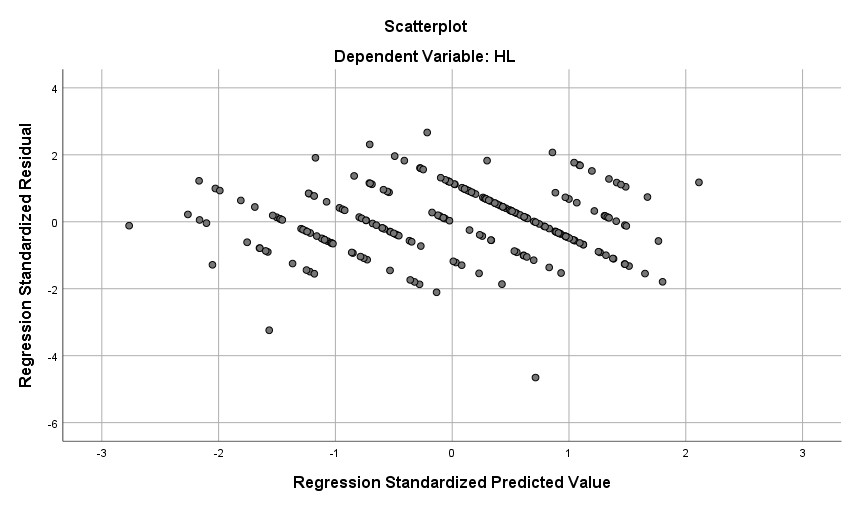
→ Phần dư chuẩn hóa phân bổ ngẫu nhiên tập trung xung quanh đường tung độ 0 tạo thành dạng đường thẳng, do vậy giả định quan hệ tuyến tính giữa biến phụ thuộc với các biến độc lập không bị vi phạm.
3. Giả định: Phương sai phần dư không thay đổi
Giả định thứ ba đó là phương sai của phần dư không thay đổi (hay còn gọi là phương sai đồng nhất). Nếu xảy ra hiện tượng phương sai thay đổi, kết quả của phương trình hồi quy sẽ không chính xác, làm sai lệch kết quả so với thực tế, từ đó khiến người nghiên cứu đánh giá nhầm chất lượng của phương trình hồi quy tuyến tính.
Để đánh giá mô hình hồi quy có vi phạm giả định này hay không, chúng ta sẽ dựa vào biểu đồ Scatter Plot giữa các phần dư chuẩn hóa và giá trị dự đoán chuẩn hóa như ở giả định liên hệ tuyến tính. Nếu các điểm phân vị phân bố khá đồng đều trên và dưới trục tung độ 0 dù X tăng hay giảm thì giả định phương sai phần dư không thay đổi không bị vi phạm.

→ Kết quả từ biểu đồ cho thấy, các điểm phân vị dao động khá đồng đều trên dưới trục tung độ 0. Các điểm phân vị hầu như nằm trong đoạn -2 đến 2 dọc theo trục tung độ 0. Do đó, giả định phương sai phần dư đồng nhất không bị vi phạm.
Bên cạnh việc dùng biểu đồ, chúng ta cũng có thể sử dụng kiểm định tương quan hạng Spearman giữa phần dư chuẩn hóa với các biến độc lập. Từ kết quả phân tích hồi quy, quay lại giao diện Data View, chúng ta sẽ thấy xuất hiện thêm một biến mới có tên là ZRE_1, đây là cột biến phần dư chuẩn hóa được SPSS xuất ra khi phân tích hồi quy. Nếu trong data bạn chưa có biến này, bạn hãy thực hiện lại phần chạy hồi quy đa biến ở bài viết này.
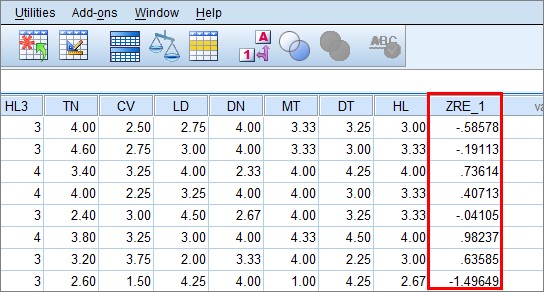
Chúng ta không làm việc trực tiếp với biến ZRE_1 mà sẽ lấy trị tuyệt đối của biến này. Vào Transform > Compute Variable…
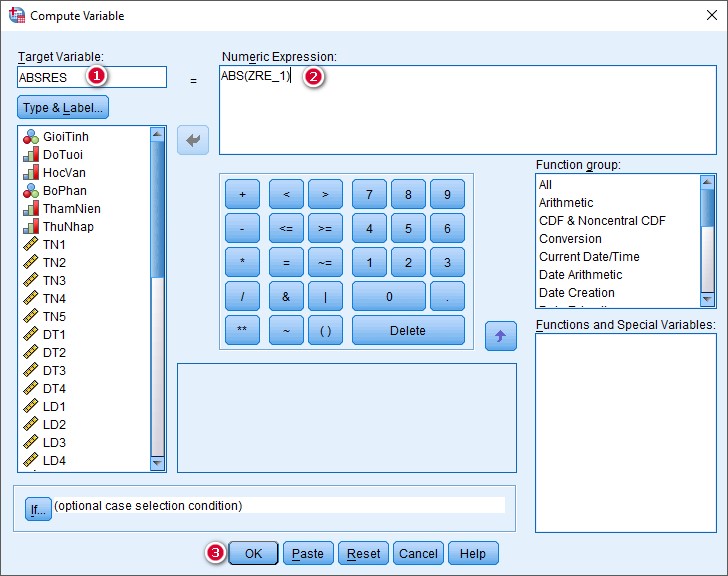
Mục Target Variable, các bạn đặt tên cho biến trị tuyệt đối của ZRE_1. Các bạn có thể đặt tên tùy ý, trong trường hợp này tác giả lấy tên ABSRES (ABS: hàm trị tuyệt đối; RES: viết tắt của Residuals, nghĩa là phần dư). Mục Numeric Expression, nhập hàm ABS(ZRE_1). Sau đó nhấp vào OK.
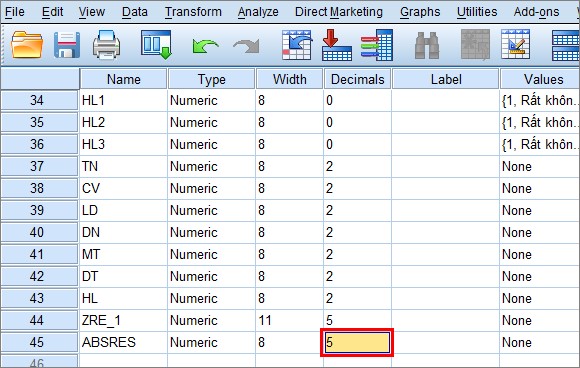
Chuyển sang giao diện Variable View, tăng giá trị Decimals của biến mới ABSRES lên 5.
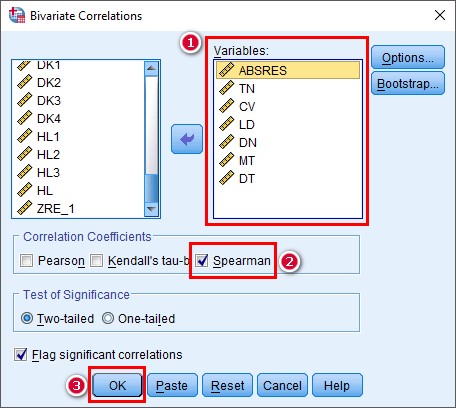
Thực hiện phân tích tương quan hạng Spearman, vào Analyze > Correlate > Bivariate…
Đưa biến ABSRES và các biến độc lập vào mục Variables. Tích chọn vào mục Spearman như hình bên dưới (nên đưa biến ABSRES lên trên cùng).
Output xuất ra bảng kết quả phân tích tương quan hạng, chúng ta sẽ chú ý tới hàng giá trị sig mối tương quan giữa ABSRES với các biến độc lập.
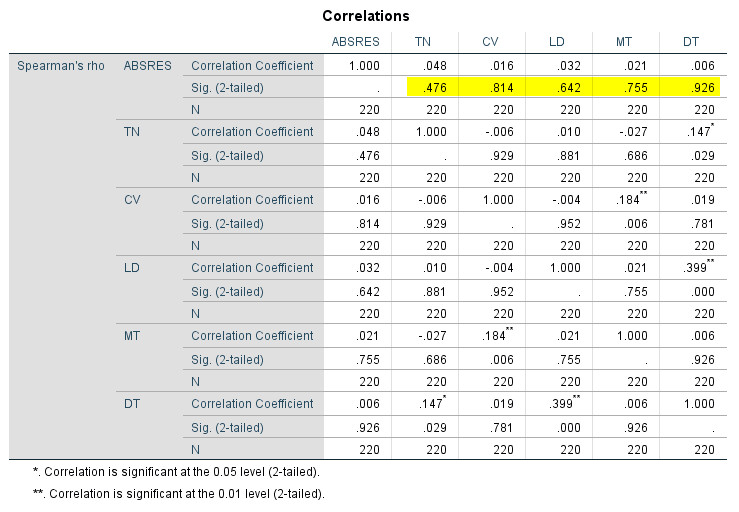
Nếu giá trị sig tương quan Spearman giữa phần dư chuẩn hóa (ABSRES) với các biến độc lập đều lớn hơn 0.05, ta có thể kết luận rằng không có hiện tượng phương sai thay đổi xảy ra, trường hợp có ít nhất 1 giá trị sig nhỏ hơn 0.05, khi đó mô hình hồi quy đã vi phạm giả định phương sai không đổi.
Nguồn tham khảo: Sử dụng tương quan hạng Spearman để kiểm định hiện tượng phương sai thay đổi trích nguồn từ Gujarati and Porter, Basic Econometrics, 5th ed., McGraw-Hill, NewYork, 2009, Chapter 11, Trang 406-407.
Nếu bạn gặp khó khăn khi kết quả hồi quy không có ý nghĩa, giá trị R2 quá thấp, các biến độc lập bị loại nhiều, vi phạm đa cộng tuyến, vi phạm các giả định hồi quy. Bạn có thể tham khảo dịch vụ xử lý số liệu SPSS của Xử Lý Định Lượng để team có thể hỗ trợ bạn xử lý nhanh và hiệu quả nhất.












