1. Lý thuyết về hồi quy tuyến tính
Hồi quy tuyến tính là phép hồi quy xem xét mối quan hệ tuyến tính – dạng quan hệ đường thẳng giữa biến độc lập với biến phụ thuộc. Khi biểu diễn bằng đồ thị scatter trên mặt phẳng Oxy để thể hiện mối quan hệ độc lập – phụ thuộc, các điểm dữ liệu có xu hướng tạo thành một đường thẳng. Đường thẳng càng rõ ràng, mô hình hồi quy càng phù hợp, càng tốt; đường thẳng càng không rõ ràng, các điểm dữ liệu phân tán càng rải rác thì mô hình hồi quy tuyến tính càng không phù hợp.
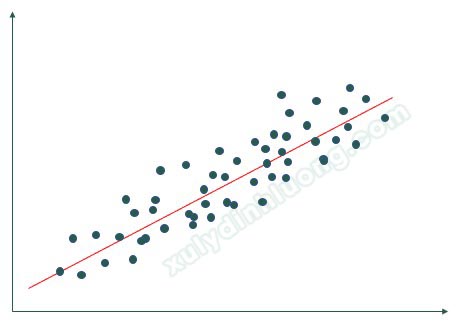
Trong nghiên cứu, chúng ta thường phải kiểm định các giả thuyết về mối quan hệ giữa hai hay nhiều biến, trong đó có một biến phụ thuộc và một hay nhiều biến độc lập. Nếu chỉ có một biến độc lập, mô hình được gọi là mô hình hồi quy đơn biến SLR (Simple Linear Regression). Trường hợp có từ hai biến độc lập trở lên, mô hình được gọi là hồi quy bội MLR (Multiple Linear Regression). Những nội dung tiếp theo ở tài liệu này chỉ đề cập đến hồi quy bội, hồi quy đơn biến tính chất tương tự với hồi quy bội.
- Phương trình hồi quy đơn biến: Y = β0 + β1X + e
- Phương trình hồi quy bội: Y = β0 + β1X1 + β2X2 + … + βnXn + e
Trong đó:
- Y: biến phụ thuộc, là biến chịu tác động của biến khác.
- X, X1, X2, Xn: biến độc lập, là biến tác động lên biến khác.
- β0: hằng số hồi quy, hay còn được gọi là hệ số chặn. Đây là chỉ số nói lên giá trị của Y sẽ là bao nhiêu nếu tất cả X cùng bằng 0. Nói cách khác, chỉ số này cho chúng ta biết giá trị của Y là bao nhiêu nếu không có các X. Khi biểu diễn trên đồ thị Oxy, β0 là điểm trên trục Oy mà đường hồi quy cắt qua.
- β1, β2, βn: hệ số hồi quy, hay còn được gọi là hệ số góc. Chỉ số này cho chúng ta biết về mức thay đổi của Y gây ra bởi X tương ứng. Nói cách khác, chỉ số này nói lên có bao nhiêu đơn vị Y sẽ thay đổi nếu X tăng hoặc giảm một đơn vị.
- e: sai số. Chỉ số này càng lớn càng khiến cho khả năng dự đoán của hồi quy trở nên kém chính xác hơn hoặc sai lệch nhiều hơn so với thực tế. Sai số trong hồi quy tổng thể hay phần dư trong hồi quy mẫu đại diện cho hai giá trị, một là các biến độc lập ngoài mô hình, hai là các sai số ngẫu nhiên.
Trong thống kê, vấn đề chúng ta muốn đánh giá là các thông tin của tổng thể. Tuy nhiên vì tổng thể quá lớn, chúng ta không thể có được các thông tin này. Vì vậy, chúng ta dùng thông tin của mẫu nghiên cứu để ước lượng hoặc kiểm định thông tin của tổng thể. Với hồi quy tuyến tính cũng như vậy, các hệ số hồi quy tổng thể như β1, β2 … hay hằng số hồi quy β0 là những tham số chúng ta muốn biết nhưng không thể đo lường được. Do đó, chúng ta sẽ sử dụng tham số tương ứng từ mẫu để ước lượng và từ đó suy diễn ra tổng thể. Phương trình hồi quy trên mẫu nghiên cứu:
Y = B0 + B1X1 + B2X2 + … + BnXn + ε
Trong đó:
- Y: biến phụ thuộc
- X, X1, X2, Xn: biến độc lập
- B0: hằng số hồi quy
- B1, B2, Bn: hệ số hồi quy
- ε: phần dư
Tất cả các nội dung hồi quy tiếp sau đây chỉ nói về hồi quy trên tập dữ liệu mẫu. Do vậy, thuật ngữ sai số sẽ không được đề cập mà chỉ nói về phần dư.
Nếu bạn gặp phải khó khăn trong thực hiện chạy phân tích hồi quy tuyến tính bội OLS, bạn không nắm vững về cách thức thao tác trên phần mềm SPSS, Xử Lý Định lượng nhận chạy SPSS, bạn có thể tham khảo dịch vụ để tối ưu về kết quả và thời gian làm bài.
2. Ước lượng hồi quy tuyến tính bằng OLS
Một trong các phương pháp ước lượng hồi quy tuyến tính phổ biến là bình phương nhỏ nhất OLS (Ordinary Least Squares). Với tổng thể, sai số (error) ký hiệu là e, còn trong mẫu nghiên cứu sai số lúc này được gọi là phần dư (residual) và được ký hiệu là ε. Biến thiên phần dư được tính bằng tổng bình phương tất cả các phần dư cộng lại. Nguyên tắc của phương pháp hồi quy OLS là làm cho biến thiên phần dư này trong phép hồi quy là nhỏ nhất. Khi biểu diễn trên mặt phẳng Oxy, đường hồi quy OLS là một đường thẳng đi qua đám đông các điểm dữ liệu mà ở đó, khoảng cách từ các điểm dữ liệu (trị tuyệt đối của ε) đến đường hồi quy là ngắn nhất.
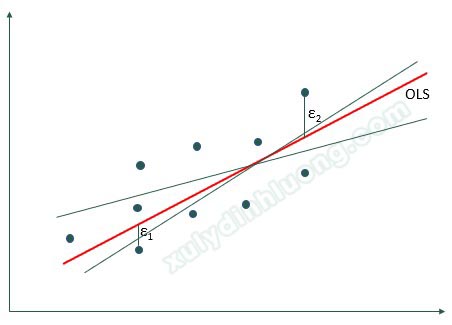
Từ đồ thị scatter biểu diễn mối quan hệ giữa các biến độc lập và biến phụ thuộc, các điểm dữ liệu sẽ nằm phân tán nhưng có xu hướng chung tạo thành dạng một đường thẳng. Chúng ta có thể có rất nhiều đường đường thẳng hồi quy đi qua đám đông các điểm dữ liệu này chứ không phải chỉ một đường duy nhất, vấn đề là ta phải chọn ra đường thẳng nào mô tả sát nhất xu hướng dữ liệu. Bình phương nhỏ nhất OLS sẽ tìm ra đường thẳng đó dựa trên nguyên tắc cực tiểu hóa khoảng cách từ các điểm dữ liệu đến đường thẳng. Trong hình ở trên đường màu đỏ là đường hồi quy OLS.












