Viết phương trình hồi quy tuyến tính trong SPSS

Trong SPSS, phương trình hồi quy tuyến tính được xác định bằng cách chạy phân tích hồi quy và lấy các hệ số từ kết quả. Cụ thể, để viết phương trình hồi quy tuyến tính trong SPSS, chúng ta sẽ sử dụng bảng hệ số hồi quy Coefficients.

1. Lý thuyết về hồi quy tuyến tính

Trong nghiên cứu, chúng ta thường kiểm định các giả thuyết về mối quan hệ giữa hai hoặc nhiều biến, bao gồm một biến phụ thuộc và một hoặc nhiều biến độc lập. Khi mô hình chỉ có một biến độc lập, đó là mô hình hồi quy đơn biến (SLR – Simple Linear Regression). Ngược lại, nếu có từ hai biến độc lập trở lên, mô hình được gọi là hồi quy bội (MLR – Multiple Linear Regression). Trong bài viết này, mình chỉ tập trung vào hồi quy bội, vì hồi quy đơn biến có tính chất tương tự.

– Phương trình hồi quy đơn biến: Y = β₀ + β₁X + e

– Phương trình hồi quy bội: Y = β₀ + β₁X₁ + β₂X₂ + … + β_nX_n + e

Trong đó:

Y: biến phụ thuộc, là biến chịu tác động của biến khác.
X, X₁, X₂, X_n: biến độc lập, là biến tác động lên biến khác.
β₀: hằng số hồi quy, hay còn được gọi là hệ số chặn. Đây là chỉ số nói lên giá trị của Y sẽ là bao nhiêu nếu tất cả X cùng bằng 0. Nói cách khác, chỉ số này cho chúng ta biết giá trị của Y là bao nhiêu nếu không có các X. Khi biểu diễn trên đồ thị Oxy, β₀ là điểm trên trục Oy mà đường hồi quy cắt qua.
β₁, β_2,β_n: hệ số hồi quy, hay còn được gọi là hệ số góc. Chỉ số này cho chúng ta biết về mức thay đổi của Y gây ra bởi X tương ứng. Nói cách khác, chỉ số này nói lên có bao nhiêu đơn vị Y sẽ thay đổi nếu X tăng hoặc giảm một đơn vị.
e: sai số. Chỉ số này càng lớn thì độ chính xác của mô hình hồi quy càng giảm, dẫn đến dự đoán kém chính xác hoặc sai lệch nhiều so với thực tế. Trong hồi quy, sai số tổng thể hoặc phần dư trong hồi quy mẫu phản ánh hai yếu tố: (1) ảnh hưởng của các biến độc lập không có trong mô hình và (2) sai số ngẫu nhiên.

Trong thống kê, mục tiêu của chúng ta là đánh giá thông tin của tổng thể. Tuy nhiên, do tổng thể quá lớn, việc thu thập đầy đủ dữ liệu là không khả thi. Vì vậy, chúng ta sử dụng thông tin từ mẫu nghiên cứu để ước lượng hoặc kiểm định đặc điểm của tổng thể. Với hồi quy tuyến tính cũng như vậy, các hệ số hồi quy tổng thể như β₁, β₂ … hay hằng số hồi quy β₀ là những tham số chúng ta muốn biết nhưng không thể đo lường được. Do đó, chúng ta sẽ sử dụng tham số tương ứng từ mẫu để ước lượng và từ đó suy diễn ra tổng thể. Phương trình hồi quy trên mẫu nghiên cứu:

Y = B₀ + B₁X₁ + B₂X₂ + … + B_nX_n + ε

Trong đó:

Y: biến phụ thuộc
X, X₁, X₂, X_n: biến độc lập
B₀: hằng số hồi quy
B₁, B_2,B_n: hệ số hồi quy
ε: phần dư

Tất cả các nội dung hồi quy tiếp sau đây chỉ nói về hồi quy trên tập dữ liệu mẫu. Do vậy, thuật ngữ sai số sẽ không được đề cập mà chỉ nói về phần dư.

2. Cách viết phương trình hồi quy trong SPSS

Thực hành phân tích hồi quy tuyến tính trên SPSS ví dụ với một tập dữ liệu gồm các biến tham gia như sau:

– Biến độc lập: GC, CSVC, SP, PV, KM

– Biến phụ thuộc: HL

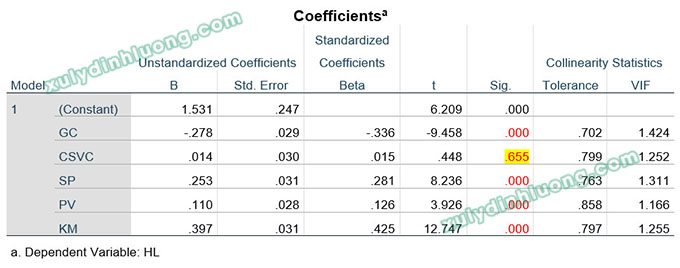
Kết quả hồi quy sẽ có bảng Coefficients như bên dưới, đây là bảng cho chúng ta các biến và tham số để viết phương trình hồi quy.

Như đã đề cập về cấu trúc của phương trình hồi quy ở phần 1, phương trình hồi quy sẽ gồm: biến phụ thuộc, biến độc lập, hằng số, hệ số hồi quy và phần dư. Trong bảng Coefficients phía trên:

Biến phụ thuộc: HL
Biến độc lập: GC, CSVC, SP, PV, KM
Hằng số: Giá trị Constant trong cột hệ số hồi quy B
Hệ số hồi quy: Cột B và Beta. SPSS cung cấp hai loại hệ số hồi quy là chưa chuẩn hóa (B) và đã chuẩn hóa (Beta).

Một số lưu ý quan trọng khi viết phương tình hồi quy:

Về ý nghĩa thống kê của biến độc lập: Nếu kết quả hồi quy cho thấy một biến độc lập không có ý nghĩa thống kê, điều này có nghĩa là biến đó không có tác động đáng kể lên biến phụ thuộc. Trong trường hợp này, không cần thiết phải loại bỏ biến và chạy lại phân tích hồi quy. Khi viết phương trình hồi quy, các biến độc lập không có ý nghĩa thống kê sẽ không được đưa vào.
Về hệ số hồi quy âm: Nếu một biến độc lập có hệ số hồi quy âm, dấu trừ (-) sẽ được giữ nguyên và đưa vào phương trình hồi quy.
Về phần dư (ε): Phần dư (ε) luôn là một thành phần của phương trình hồi quy, bất kể phương trình đó đã được chuẩn hóa hay chưa.
Về phương trình hồi quy chuẩn hóa: Phương trình hồi quy chuẩn hóa sẽ không có hằng số. Điều này là do quá trình chuẩn hóa các hệ số hồi quy đã loại bỏ hằng số.

3. Thực hành viết phương trình hồi quy trong SPSS

Tiến hành viết phương trình hồi quy dựa vào bảng Coefficients bên dưới:

Phân tích các điểm lưu ý:

– Biến CSVC có giá trị sig kiểm định t bằng 0.655 > 0.05, biến này không có ý nghĩa trong mô hình hồi quy, do đó chúng ta không đưa biến này vào phương trình.

– Biến GC có hệ số hồi quy mang dấu âm, biến này tác động nghịch chiều lên biến phụ thuộc HL. Khi viết phương trình, chúng ta sẽ mang cả dấu âm này vào.

Tiến hành viết phương trình:

Vì SPSS cung cấp hai loại hệ số hồi quy: hệ số chưa chuẩn hóa B (Unstandardized Coefficients) và hệ số đã chuẩn hóa β (Standardized Coefficients – Beta), chúng ta có thể viết hai phương trình hồi quy tương ứng. Tuy nhiên, khi cần trình bày một phương trình hồi quy hoàn chỉnh hoặc khi được hỏi về phương trình hồi quy của mô hình, chúng ta sẽ sử dụng phương trình hồi quy với hệ số chưa chuẩn hóa.

Phương trình hồi quy chưa chuẩn hóa:

HL = 1.531 – 0.278*GC + 0.253*SP + 0.110*PV + 0.397*KM + ε

Phương trình hồi quy chuẩn hóa:

HL = -0.336*GC + 0.281*SP + 0.126*PV + 0.425*KM + ε