Trong phần mềm SMARTPLS, bên cạnh chỉ số Cronbach’s Alpha, hai chỉ số độ tin cậy tổng hợp là Composite Reliability rho_c và Composite Reliability rho_a cũng được sử dụng để đánh giá độ tin cậy của thang đo. Vậy, điểm khác biệt giữa Composite Reliability rho_c và Composite Reliability rho_a là gì?
1. Độ tin cậy tổng hợp Composite Reliability rho_c
1.1 Định nghĩa
Độ tin cậy tổng hợp rho_c, thường được biết đến với tên gọi Composite Reliability, được Karl Jöreskog giới thiệu vào năm 1971 trong bối cảnh phân tích mô hình phương trình cấu trúc (SEM).
Chỉ số rho_c là một thước đo độ tin cậy nội tại của thang đo, phản ánh mức độ nhất quán giữa các biến quan sát (items) trong việc đo lường một khái niệm tiềm ẩn (construct). Mục tiêu chính của rho_c là xác định xem các biến quan sát có cùng đo lường một khái niệm chung hay không.
Hiện nay, rho_c vẫn được xem là một chỉ số quan trọng trong việc đánh giá độ tin cậy của thang đo trong các nghiên cứu sử dụng SEM, đặc biệt là khi ứng dụng trên các phần mềm như SMARTPLS và AMOS.
1.2 Công thức tính rho_c
Công thức tính rho_c dựa trên hệ số tải trọng (loadings) của từng biến quan sát trong mô hình:
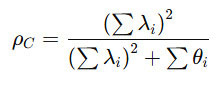
Trong đó:
- λ𝑖: là hệ số tải trọng (factor loading) của biến quan sát 𝑖.
- 𝜃𝑖: là phương sai của phần dư (error variance) của biến quan sát 𝑖.
Jöreskog phát triển chỉ số rho_c như một phương án thay thế cho Cronbach’s Alpha (α), do hạn chế của Alpha trong việc giả định rằng tất cả các biến quan sát có tải trọng bằng nhau—một giả định thường không phù hợp với thực tế nghiên cứu. Ngược lại, rho_c cho phép các biến quan sát có tải trọng khác nhau, từ đó cung cấp một ước lượng độ tin cậy chính xác và linh hoạt hơn cho thang đo.
1.3 Ngưỡng chấp nhận
Không chỉ rho_c, mà cả Cronbach’s Alpha và rho_a (sẽ được trình bày ở phần sau) đều là các chỉ số dùng để đánh giá tính nhất quán nội tại của các biến quan sát trong một thang đo. Các chỉ số này thường áp dụng ngưỡng chấp nhận tối thiểu là 0.7 theo khuyến nghị của Nunnally và Bernstein (1994) cũng như Hair và cộng sự (2022); trong khi đó, đối với các nghiên cứu mang tính khám phá, ngưỡng 0.6 vẫn được xem là chấp nhận được.
2. Độ tin cậy tổng hợp Composite Reliability rho_a
2.1. Định nghĩa
Độ tin cậy tổng hợp rho_a (hay còn gọi là Dijkstra-Henseler’s rho) là một chỉ số dùng để đo lường độ tin cậy tổng hợp của tập hợp các biến quan sát trong mô hình PLS-SEM. Chỉ số này được phát triển nhằm khắc phục những hạn chế về độ chính xác của các chỉ số truyền thống như Cronbach’s Alpha và rho_c (Jöreskog’s rho).
Hệ số độ tin cậy này khuyến khích sử dụng khi nhà nghiên cứu sử dụng thuật toán ước lượng Consistent PLS-SEM (PLSc-SEM).
Ban đầu, chỉ số này được gọi đơn giản là rho_a. Tuy nhiên, một số tài liệu về PLS-SEM sau này đã bổ sung thêm cụm từ Composite Reliability, gọi là Composite Reliability rho_a, nhằm phân biệt rõ hơn với Composite Reliability rho_c. Trên phần mềm SMARTPLS, ký hiệu này cũng có sự thay đổi: nếu như phiên bản SMARTPLS 3 chỉ ghi là rho_a, thì từ phiên bản SMARTPLS 4, chỉ số này được hiển thị dưới dạng đầy đủ là Composite Reliability rho_a.
2. Công thức tính rho_a
Dijkstra và Henseler (2015) đề xuất tính rho_a dựa trên ma trận hiệp phương sai giữa các chỉ báo. Công thức gốc của rho_a thực sự phức tạp, dưới đây là công thức tổng quát của chỉ số này.
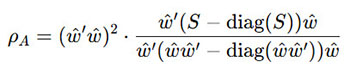
Trong đó:
- w: vector hệ số trọng số ngoài (outer weights) của các biến quan sát
- w’: chuyển vị của vector w
- S: ma trận hiệp phương sai mẫu của các biến quan sát
- diag(S): ma trận chỉ giữ lại các phần tử đường chéo của S → đại diện cho phương sai riêng của từng biến quan sát
- S − diag(S): phần hiệp phương sai chung giữa các biến quan sát
- w * w’: ma trận tích ngoài của vector trọng số w
- diag(w * w’): ma trận chỉ giữ phần tử đường chéo của w * w’
- w * w’ − diag(w * w’): phần tương tác giữa các trọng số khác nhau
Dựa theo công thức tính rho_a, hệ số này có thể nằm ngoài khoảng dao động từ 0 đến 1 (Takane and Hwang, 2018).
3. Khác biệt Composite Reliability rho_c và rho_a là gì?
3.1 So sánh Cronbach’s Alpha, Composite Reliability rho_c và rho_a
SMARTPLS cung cấp ba chỉ số để đánh giá độ tin cậy của thang đo, hay còn gọi là độ tin cậy nhất quán nội bộ, bao gồm: Cronbach’s Alpha, Composite Reliability rho_a, và Composite Reliability rho_c.
Theo Hair và cộng sự (2022), Cronbach’s Alpha có xu hướng đánh giá thấp độ tin cậy, trong khi Composite Reliability rho_c lại đánh giá quá cao. Do đó, độ tin cậy thực tế của cấu trúc tiềm ẩn thường được xem là nằm giữa hai giá trị này.
Trong bối cảnh đó, rho_a thường có giá trị nằm giữa Cronbach’s Alpha và rho_c, và vì vậy được xem là chỉ số phản ánh chính xác hơn độ tin cậy tổng hợp (Hair et al., 2022). Đây cũng chính là điểm khác biệt cốt lõi giữa Composite Reliability rho_a và rho_c.
3.2 Các chỉ số độ tin cậy trên SMARTPLS 3, SMARTPLS 4
Trên phiên bản SMARTPLS 3 và SMARTPLS 4, giá trị Cronbach’s Alpha, Composite Reliability rho_c, Composite Reliability rho_a sẽ nằm trong bảng Construct Reliability and Validity thuộc phân tích PLS-Algorithm.
Chúng ta sẽ nhận xét và trình bày kết quả hai hệ số này trong phần đánh giá mô hình đo lường trên SMARTPLS.
Giao diện trên phiên bản SMARTPLS 3:
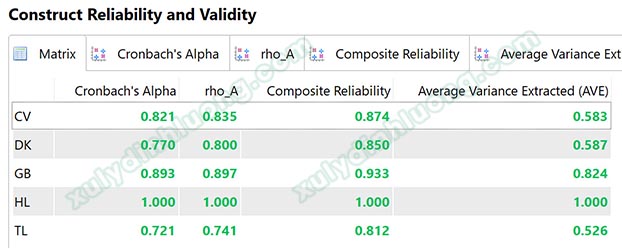
Thang đo HL trong kết quả trên có Cronbach’s Alpha, Composite Reliability rho_c, Composite Reliability rho_a đều bằng 1 vì đây là thang đo chỉ có một biến quan sát. Thang đo chỉ có một biến quan sát mặc định sẽ có Cronbach’s Alpha, Composite Reliability rho_c, Composite Reliability rho_a luôn bằng 1 trong SMARTPLS 3.
Giao diện trên phiên bản SMARTPLS 4:
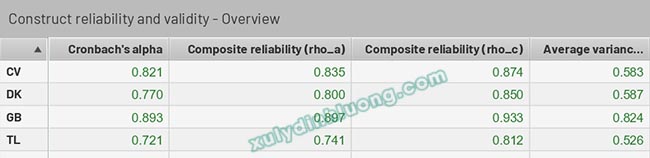
Trên phiên bản SMARTPLS 4, cấu trúc chỉ có một biến quan sát sẽ không hiển thị các chỉ số độ tin cậy.
Ở kết quả ví dụ minh họa phía trên có thể thấy rho_a luôn có giá trị cao hơn Cronbach’s Alpha và thấp hơn rho_c.
—
Nguồn tham khảo:
Nunally và Bernstein (1994), The Assessment of Reliability. Psychometric Theory, 3, 248-292.
Hair và cộng sự (2022), A primer on partial least squares structural equation modeling (PLS-SEM), 3rd ed., Thousand Oaks, CA: Sage.












