Trong phân tích hồi quy, hệ số R bình phương hiệu chỉnh là một chỉ số quan trọng để đánh giá mức độ phù hợp của mô hình. Tuy nhiên, không có một ngưỡng giá trị cụ thể nào được quy định cho hệ số này. Nếu giá trị R bình phương hiệu chỉnh quá thấp, điều này có thể gợi ý rằng mô hình hồi quy chưa thực sự phù hợp với dữ liệu. Trong tình huống này, chúng ta nên xem xét áp dụng các kỹ thuật xử lý dữ liệu để tăng giá trị R bình phương hiệu chỉnh trong SPSS.
1. So sánh R bình phương và R bình phương hiệu chỉnh
R bình phương (R-squared)
- Định nghĩa: R bình phương thể hiện tỷ lệ phương sai của biến phụ thuộc (dependent variable) được giải thích bởi các biến độc lập (independent variables) trong mô hình hồi quy.
- Giá trị: R bình phương có giá trị từ 0 đến 1. Giá trị càng gần 1, mô hình càng phù hợp, tức là các biến độc lập càng giải thích được nhiều sự biến thiên của biến phụ thuộc. Ngược lại, giá trị càng gần 0, mô hình càng ít phù hợp.
- Ưu điểm: Dễ hiểu và tính toán.
- Nhược điểm: R bình phương có xu hướng tăng khi bạn thêm nhiều biến độc lập vào mô hình, kể cả khi các biến đó không thực sự có ý nghĩa. Điều này có thể dẫn đến việc đánh giá sai lệch về mức độ phù hợp của mô hình.
R bình phương hiệu chỉnh (Adjusted R-squared)
- Định nghĩa: R bình phương hiệu chỉnh là một phiên bản điều chỉnh của R bình phương, được tính toán để xem xét số lượng biến độc lập trong mô hình.
- Giá trị: R bình phương hiệu chỉnh cũng có giá trị từ 0 đến 1, nhưng thường nhỏ hơn R bình phương.
- Ưu điểm: R bình phương hiệu chỉnh không tăng khi bạn thêm các biến độc lập không có ý nghĩa vào mô hình. Nó giúp bạn đánh giá chính xác hơn về mức độ phù hợp của mô hình, đặc biệt khi so sánh các mô hình với số lượng biến độc lập khác nhau.
- Nhược điểm: Khó hiểu và tính toán hơn R bình phương.ệu thực tế. Hai giá trị này càng gần 1, mô hình càng phù hợp, tức là các biến độc lập càng giải thích được nhiều sự biến thiên của biến phụ thuộc. Ngược lại, hai giá trị này càng gần 0, mô hình càng ít phù hợp.
2. R bình phương hiệu chỉnh dưới 0.5 (50%)
R bình phương hiệu chỉnh dưới 0.5 có thể cho thấy mô hình hồi quy không giải thích được nhiều về phương sai của biến phụ thuộc. Tuy nhiên, việc này có thực sự là vấn đề hay không còn phụ thuộc vào bối cảnh nghiên cứu và lĩnh vực ứng dụng. Quan điểm cho rằng mức R bình phương hoặc R bình phương hiệu chỉnh dưới 0.5 thì kết quả hồi quy không có ý nghĩa là không chính xác.
Khi R bình phương hiệu chỉnh có giá trị quá thấp (gần 0), điều này có thể gợi ý một số vấn đề sau:
- Mô hình chưa phù hợp: Có thể mô hình hồi quy chưa thực sự phù hợp với dữ liệu. Các biến độc lập được sử dụng chưa giải thích được nhiều sự biến thiên của biến phụ thuộc.
- Thiếu biến quan trọng: Có thể mô hình thiếu các biến độc lập quan trọng, ảnh hưởng đến biến phụ thuộc.
- Mối quan hệ phức tạp: Mối quan hệ giữa các biến có thể phức tạp hơn so với giả định của mô hình hồi quy tuyến tính.
- Sai số lớn: Sai số của mô hình có thể lớn, làm giảm độ chính xác của các ước lượng.
Không có tiêu chuẩn quy định R bình phương hay R bình phương hiệu chỉnh ở mức bao nhiêu thì mô hình mới đạt yêu cầu. Hai giá trị này chấp nhận được phụ thuộc vào nhiều yếu tố, bao gồm:
- Lĩnh vực nghiên cứu: Trong một số lĩnh vực, R bình phương trên 0.3 đã được coi là tốt, trong khi ở các lĩnh vực khác, giá trị này trên 0.9 mới được coi là chấp nhận được.
- Mục đích của nghiên cứu: Nếu mục đích của nghiên cứu là dự đoán, R bình phương cao là quan trọng hơn. Nếu mục đích là giải thích mối quan hệ giữa các biến, R bình phương có thể thấp hơn.
- Độ phức tạp của mô hình: Mô hình càng phức tạp (có nhiều biến độc lập), R bình phương càng có xu hướng cao hơn. Tuy nhiên, điều này không có nghĩa là mô hình đó tốt hơn.
3. Cách tăng giá trị R bình phương hiệu chỉnh trong SPSS
3.1 Tăng R bình phương hiệu chỉnh bằng đồ thị Scatter Plot hồi quy
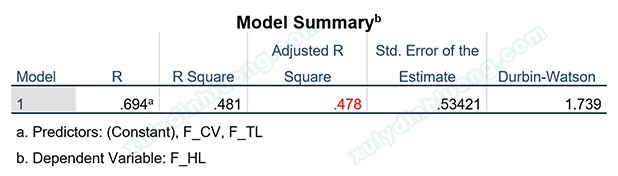
Xét ví dụ phép phân tích hồi quy bên dưới với hai biến độc lập F_TL và F_CV tác động vào biến phụ thuộc F_HL. Giá trị R bình phương hiệu chỉnh Adjusted R Square trong bảng Model Summary bằng 0.478. Đây là một chỉ số thể hiện mức độ phù hợp của mô hình hồi quy, chỉ số này càng tiến về 1, càng cho thấy mô hình hồi quy là phù hợp.
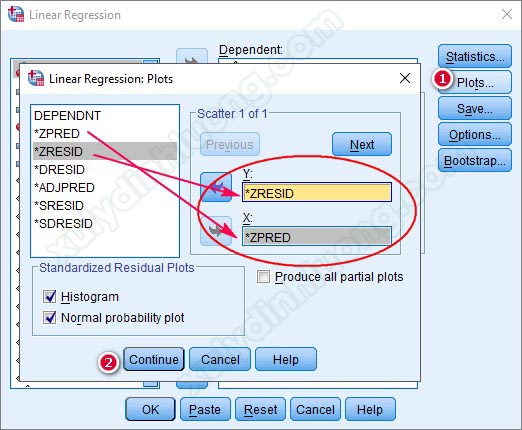
Để xuất hiện được đồ thị Scatter, khi thực hiện phân tích hồi quy tuyến tính bội, các bạn vào mục Plots, tích chọn kéo biến ZRESID thả vào ô Y, kéo biến ZPRED thả vảo ô X như hình bên dưới.
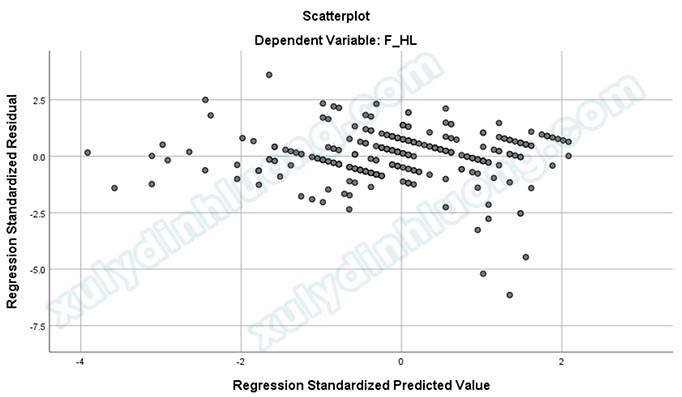
Các bạn nên phân tích hồi quy chính xác theo hướng tại bài viết Phân tích và đọc kết quả hồi quy tuyến tính bội trên SPSS để xuất ra đầy đủ các bảng, đồ thị cần dùng cho nhận xét kết quả, bao gồm cả đồ thị Scatter.
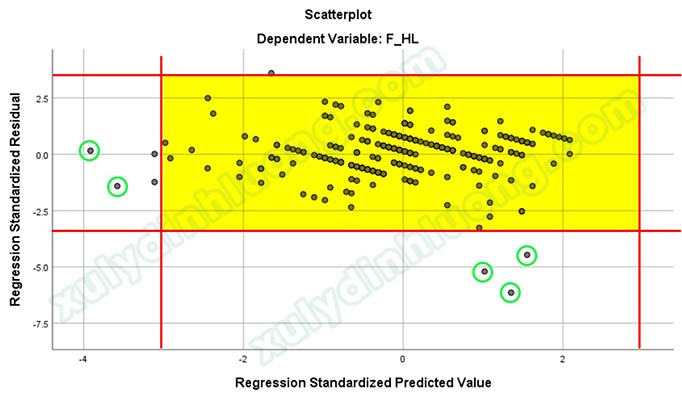
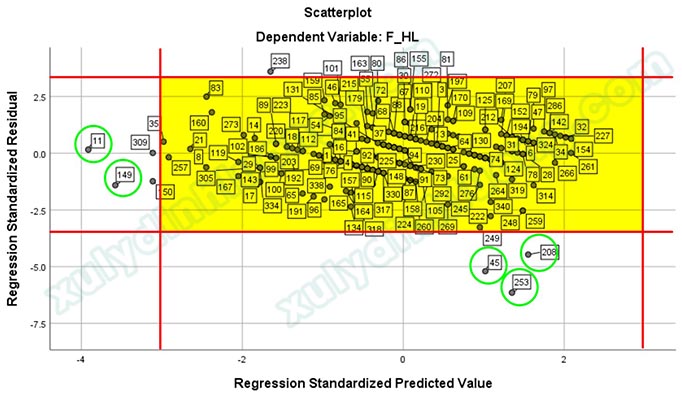
Theo quy luật Empirical hay còn gọi là quy luật 68-95-99.7 trong phân phối chuẩn, các điểm dữ liệu nằm ngoài vùng -3 đến 3 ở cả hai trục hoành và trục tung sẽ là các điểm dị biệt (phần giải thích sẽ được trình bày ở mục kế tiếp). Nếu kết quả hồi quy không tốt, chúng ta nên xem xét loại bỏ các điểm này để cải thiện mô hình. Có năm điểm đánh dấu bằng màu xanh lá nằm ngoài khu vực tô vàng chính là các điểm dị biệt.
Chúng ta sẽ yêu cầu phần mềm hiện tên quan sát của điểm dữ liệu để xác định ID của năm điểm dị biệt trên bằng cách nhấp đôi chuột vào đồ thị, chọn vào biểu tượng khoanh tròn như ảnh bên dưới, sau đó nhấp vào nút Close để đóng cửa sổ.
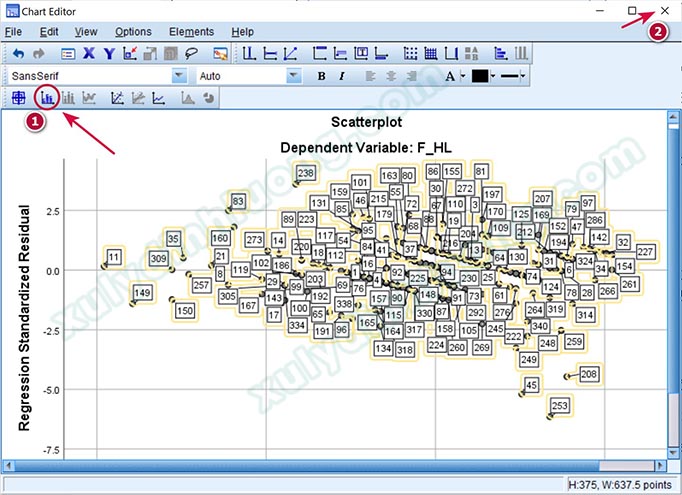
Như vậy, năm điểm dị biệt được xác định là các quan sát: 11, 149, 45, 208, 253.
Chúng ta sẽ xóa 5 hàng 11, 149, 45, 208, 253 trong dữ liệu. Lưu ý rằng, bạn nên tạo một cột dữ liệu số thứ tự để xóa cho chính xác vị trí các hàng. Khi xóa dữ liệu, cần xóa từ hàng có thứ tự cao tới hàng có thứ tự thấp. Thực hiện hồi quy tuyến tính bội với tập dữ liệu đã được loại bỏ các quan sát dị biệt để xem xét sự thay đổi.
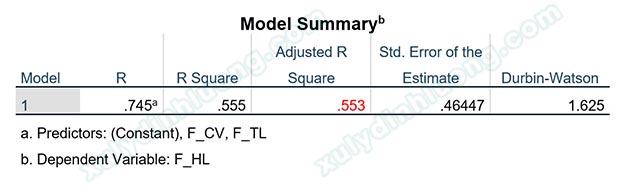
Giá trị Adjusted R Square mới bằng 0.553, lớn hơn rất nhiều so với giá trị ban đầu 0.478, độ phù hợp mô hình hồi quy đã cải thiện rất đáng kể. Đánh đổi sự cải thiện này, chúng ta loại đi 5 quan sát dị biệt. Số lượng 5 quan sát so với cỡ mẫu 350 là rất nhỏ, do vậy, chúng ta nên loại bỏ các quan sát dị biệt này để có được kết quả hồi quy tốt hơn.
Nếu bạn gặp khó khăn khi thực hiện phân tích hồi quy vì số liệu khảo sát không tốt, vi phạm các tiêu chí kiểm định. Bạn có thể tham khảo dịch vụ chạy SPSS của Phạm Lộc Blog hoặc zalo 093 395 1549 để tối ưu thời gian làm bài và đạt kết quả tốt hơn nhé.
3.2 Tăng R bình phương hiệu chỉnh bằng bảng Casewise Diagnostics
Khi thực hiện phân tích hồi quy tuyến tính, SPSS có chức năng nhận diện tự động điểm dị biệt. Để làm được điều này, trong tùy chọn Statistics, chúng ta tích vào mục Casewise diagnostics và nhập giá trị 2 hoặc 3 standard deviation (độ lệch chuẩn) vào ô Outliers outside. Thường chúng ta sẽ xét điểm dị biệt ngoài vùng 3 độ lệch chuẩn trước, nếu xử lý xong các điểm dị biệt này nhưng kết quả vẫn không khả quan, chúng ta mới xét điểm dị biệt ngoài vùng 2 độ lệch chuẩn.
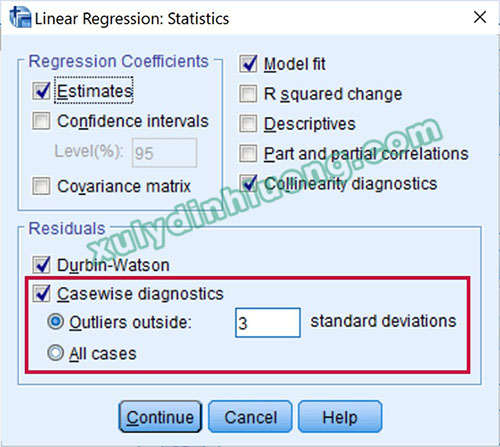
Tiếp tục thực hành phân tích hồi quy tác động từ F_TL, F_CV lên F_HL. Tại Casewise diagnostics nhập giá trị 3 để phát hiện điểm dị biệt nằm ngoài vùng 3 độ lệch chuẩn. Kết quả hồi quy cho chúng ta giá trị Adjusted R Square bằng 0.478 và bảng Casewise Diagnostics chứa các quan sát dị biệt gồm: 45, 208, 238, 249, 253.
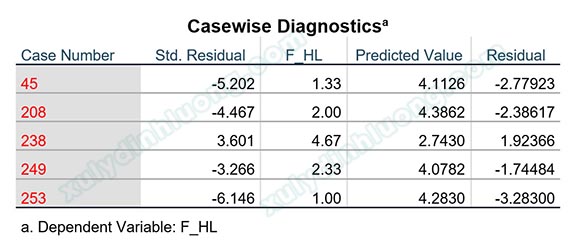
Chúng ta sẽ xóa 5 hàng 45, 208, 238, 249, 253 trong dữ liệu. Lưu ý rằng, bạn nên tạo một cột dữ liệu số thứ tự để xóa cho chính xác vị trí các hàng. Khi xóa dữ liệu, cần xóa từ hàng có thứ tự cao tới hàng có thứ tự thấp. Thực hiện hồi quy tuyến tính bội với tập dữ liệu đã được loại bỏ các quan sát dị biệt để xem xét sự thay đổi.
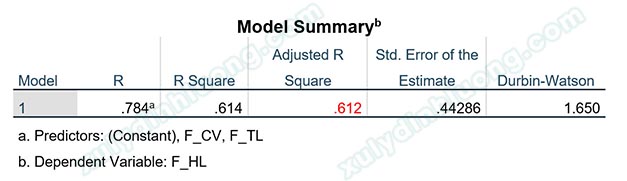
Giá trị Adjusted R Square mới bằng 0.612 > 0.478. Có thể thấy độ phù hợp của mô hình đã tốt hơn rất nhiều sau khi loại bỏ 5 quan sát dị biệt.
