Đánh giá độ phù hợp mô hình Binary Logistic

Hồi quy Binary Logistic là mô hình phổ biến trong nghiên cứu dùng để ước lượng xác suất một sự kiện sẽ xảy ra. Đặc trưng của hồi quy này là biến phụ thuộc chỉ có hai giá trị: 0 và 1. Cũng như hồi quy tuyến tính bội, trong hồi quy nhị phân Binary Logistic chúng ta cũng sẽ có những chỉ số để đánh giá độ phù hợp mô hình. 

1. Giả thuyết độ phù hợp mô hình

Trước khi xem xét mức độ phù hợp mạnh/yếu, chúng ta sẽ cần xem mô hình có ý nghĩa hay không. Trong hồi quy tuyến tính, chúng ta sử dụng kiểm định F để kiểm định giả thuyết ý nghĩa của mô hình (sự phù hợp của mô hình), còn với hồi quy Binary Logistic chúng ta sẽ sử dụng kiểm định Chi-square. Giả thuyết H₀: Không có khác biệt giữa mô hình trống và mô hình đề xuất. Phép kiểm định Chi-square được sử dụng để kiểm định giả thuyết này. Kết quả kiểm định:

• Sig < 0.05: Bác bỏ giả thiết H₀, nghĩa là có khác biệt giữa mô hình trống và mô hình đề xuất một cách có ý nghĩa thống kê, mô hình hồi quy là phù hợp.
• Sig > 0.05: Chấp nhận giả thiết H₀, nghĩa là không có khác biệt giữa mô hình trống và mô hình đề xuất một cách có ý nghĩa thống kê, mô hình hồi quy không phù hợp.

Hướng tiếp cận của kiểm định Chi-square trong đánh giá độ phù hợp mô hình hồi quy nhị phân Binary Logistic đó là so sánh sự khác biệt giá trị -2LL giữa mô hình hồi quy trống và mô hình hồi quy được đề xuất, nếu mô hình đề xuất có -2LL thấp hơn mô hình trống sẽ là kết quả tốt. Trong SPSS, kết quả tính toán của mô hình hồi quy trống sẽ được thể hiện ở Block 0. Sau đó, các biến độc lập được đưa vào mô hình tạo nên mô hình hồi quy đề xuất. SPSS sẽ xử lý mô hình hồi quy đề xuất và đánh giá xem có sự khác biệt có ý nghĩa thống kê trị số -2LL giữa mô hình trống với mô hình đề xuất hay không, kết quả đánh giá sẽ được thể hiện ở Block 1.

Các số liệu của kiểm định Chi-square được lấy từ bảng Omnibus Tests of Model Coefficients. Bảng này sẽ có ba mục: Step, Block, Model. Chúng ta sẽ chú trọng vào kết quả kiểm định Chi-square ở mục Model, hai mục Step và Block chúng ta sẽ đánh giá bổ sung thêm cho Model nếu sử dụng các phép đưa biến vào là Forward, Backward.

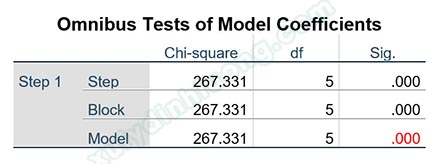
2. Hệ số -2 Log-Likelihood (-2LL)

Trong hồi quy tuyến tính, chúng ta đánh giá mức độ phù hợp của mô hình qua hệ số xác định R² (R square). Một mô hình hồi quy tuyến tính càng phù hợp khi R² càng lớn và phần dư ε càng nhỏ. Tương tự vậy đặc điểm của phần dư ε, với hồi quy Binary Logistic, chúng ta có giá trị log-likelihood. Log-likelihood đại diện cho phần thông tin không được giải thích bởi mô hình hồi quy Binary Logistic, nếu chỉ số này càng lớn, mô hình càng không phù hợp (Andy Field, 2009)[1].

Công thức tính của log-likelihood không thuận tiện cho việc đọc kết quả. Chính vì vậy, các nhà nghiên cứu đã sử dụng phép chuyển đổi toán học để đưa hệ số này về dạng -2 log-likelihood (-2LL), giá trị này cũng sẽ được thể hiện trong kết quả hồi quy Binary Logistic trên SPSS thay vì giá trị log-likelihood. Chúng ta sẽ không cần quan tâm quá trình chuyển đổi này thế nào, chỉ cần nhớ rằng, -2LL cũng như log-likelihood có tính chất tương tự phần dư ε trong hồi quy tuyến tính, chỉ số này càng nhỏ mô hình hồi quy nhị phân càng phù hợp. Trị số -2LL có giá trị nhỏ nhất là 0 và không có giá trị lớn nhất. -2LL thường ứng dụng để so sánh giữa mô hình hồi quy trống (Null Model) và mô hình hồi quy được đề xuất (Proposed Model), nếu mô hình đề xuất có -2LL thấp hơn mô hình trống thì kết quả hồi quy là tốt (Hair và cộng sự, 2014). Mô hình hồi quy trống nghĩa là không có biến độc lập nào được đưa vào mô hình. Mô hình hồi quy đề xuất là mô hình có sự xuất hiện của các biến độc lập. Tùy vào phép đưa biến (Enter hay Stepwise) mà sẽ có một hay nhiều mô hình hồi quy đề xuất, nhưng thường chúng ta xét đến mô hình hồi quy đề xuất cuối cùng.

Xem cách đọc chỉ số -2LL tại bài viết: Hồi quy nhị phân Binary Logistic trong SPSS

3. Hệ số Cox & Snell R Square và Nagelkerke R Square

Hệ số -2LL gây khó khăn cho việc nhận xét mức độ phù hợp mô hình hồi quy nhị phân bởi không có ngưỡng tiêu chuẩn. Do vậy, các nhà nghiên cứu tìm kiếm thêm các giải pháp khác để có thêm nhiều tiêu chí đánh giá mô hình hồi quy Binary Logistic. Một trong các giải pháp đó là xây dựng giá trị “R Square giả” (Pseudo R Square) dựa theo tính chất R Square trên hồi quy tuyến tính (Hair và cộng sự, 2014)[2]. Hai giá trị R Square cho hồi quy Binary Logistic mà SPSS sử dụng dựa trên nghiên cứu của Cox & Snell (1989)[3] và Nagelkerke (1991)[4]. Theo công thức tính, hệ số Cox & Snell R Square sẽ không thể đạt tới giá trị lớn nhất là 1. Vì vậy, Nagelkerke đã đưa ra thêm một chỉ số R Square khác có giá trị dao động từ 0 đến 1. Cả hai trị số R Square này nếu càng lớn thì độ phù hợp mô hình hồi quy nhị phân Binary Logistic càng cao.

[1] Andy Field, Discovering Statistics using SPSS, Sage, London, 2009.

[2] Hair và cộng sự, Multivariate Data Analysis, Pearson, New Jersey, 2014.

[3] Cox & Snell, Analysis of Binary Data, Chapman and Hall/CRC, London, 1989.

[4] Nagelkerke, A note on the general definition of the coefficient of determination, Biometrika, 1991.