Để đánh giá mô hình đo lường dạng kết quả trên SMARTPLS 3, chúng ta sẽ tập trung vào các vấn đề xoay quanh chất lượng của các biến quan sát (outer loading), độ tin cậy cấu trúc thang đo (cronbach’s alpha, composite reliability), tính hội tụ (convergent validity), tính phân biệt (discriminant validity) và độ phù hợp mô hình (model fit). Nếu bạn đang sử dụng mô hình đo lường dạng
1. Thiết lập phân tích mô hình ước lượng trên SMARTPLS 3
Tại giao diện diagram, chúng ta nhấp vào Calculate > PLS Algorithm. Lưu ý, nút này chỉ xuất hiện khi chúng ta đang ở cửa số diagram hình vẽ mô hình đường dẫn.
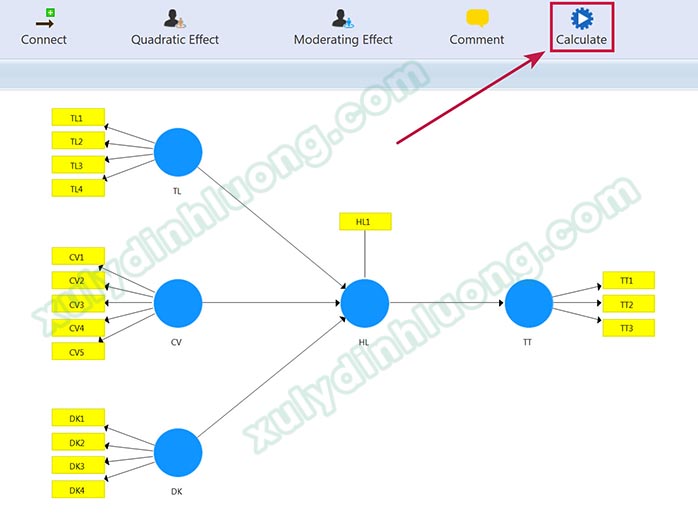
Bài viết này sẽ sử dụng các thuật ngữ của PLS-SEM, để hiểu được chính xác nội dung, bạn vui lòng xem trước bài viết Mô hình cấu trúc và mô hình đo lường trong PLS-SEM. Cửa sổ Partial Least Squares Algorithm xuất hiện, tiến hành thiết lập phân tích mô hình ước lượng SMARTPLS như sau:
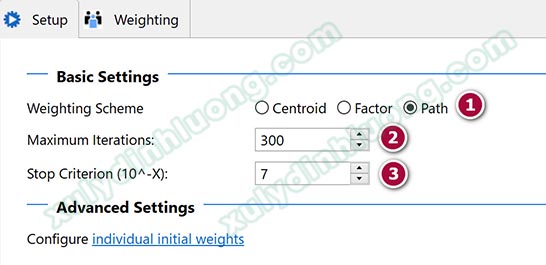
– Weighting Scheme: Chọn Path vì phương pháp “lược đồ trong số đường dẫn – path weighting là phương pháp tối ưu hơn hai phương pháp còn lại bởi nó cung cấp hệ số R bình phương cao nhất cho từng mô hình đường dẫn (Lohmoller, 1989) và có thể áp dụng cho mọi loại mô hình PLS-SEM (Henseler và cộng sự, 2012).
– Maximum Iterations: Mặc định của phần mềm là 300. Đặc tính thuật toán PLS là một quá trình lặp của phương pháp hồi quy bình phương tối thiểu nhỏ nhất với mục tiêu tìm ra trọng số ngoài outer weight (hệ số hồi quy) của các biến quan sát để tính toán giá trị biến tiềm ẩn. Số vòng lặp sẽ dừng nếu giá trị trọng số ngoài của mô hình đạt được sự hội tụ. Nếu số bước lặp vượt quá 300, mô hình không tính toán được trọng số ngoài các biến quan sát, từ đó không thể tìm ra được “mối liên hệ trọng số” giữa biến tiềm ẩn và các biến quan sát.
– Stop Criterion(10^-X): Mặc định của phần mềm là 7. Đây là tiêu chuẩn ngưỡng dừng của quá trình lặp. Hair và cộng sự (2016) đề xuất giá trị này là 5, hoặc 7, SMARTPLS sử dụng ngưỡng 7 làm mặc định.
Tiếp tục nhấp vào Start Calculation để tiến hành phân tích.

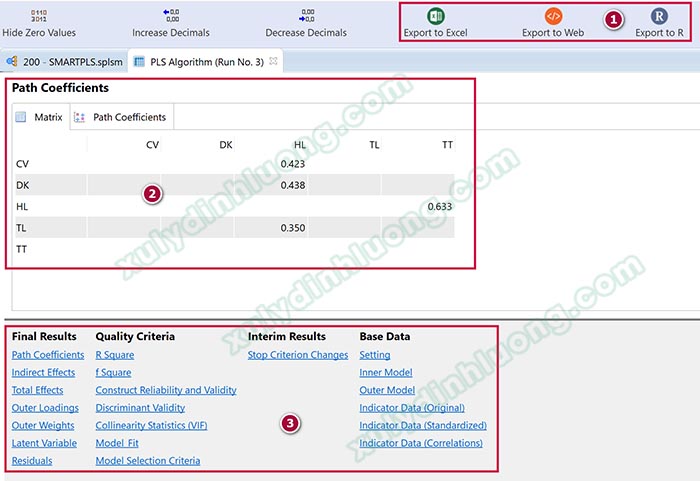
Output kết quả PLS Algorithm xuất hiện, chúng ta sẽ quan tâm đến 3 mục như ảnh bên dưới. Mục số 1, Export to Excel, Web, R để chúng ta xuất kết quả output ra file excel, file html hoặc định dạng của phần mềm R. Mục số 2 là giao diện hiển thị kết quả khi chúng ta nhấp vào các đầu mục kết quả ở mục 3. Mục số 3 là danh sách các kết quả phân tích mô hình.
2. Đánh giá mô hình đo lường trên SMARTPLS 3
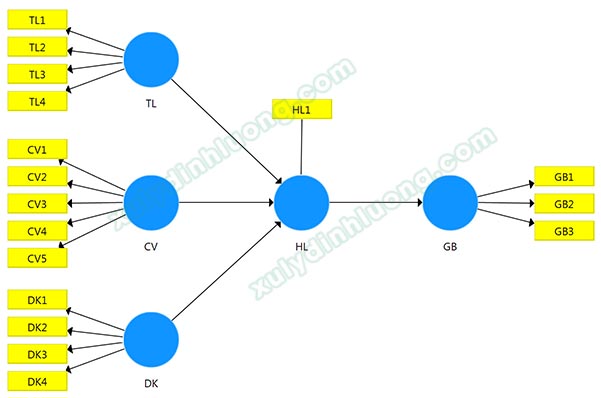
Phần hướng dẫn thực hiện đánh giá mô hình đo lường measurement model bên dưới sẽ sử dụng tập dữ liệu của một nghiên cứu có mô hình như sau:
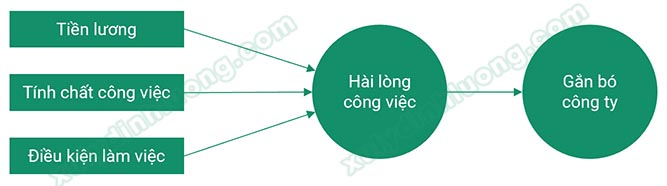
Mỗi biến tiềm ẩn trong mô hình được đo thông qua tập hợp biến quan sát như sau:
– Tiền lương (TL) gồm TL1, TL2, TL3, TL4.
– Tính chất công việc (CV) gồm CV1, CV2, CV3, CV4, CV5.
– Điều kiện làm việc (DK) gồm DK1, DK2, DK3, DK4.
– Hài lòng công việc (HL) gồm duy nhất chỉ một biến quan sát HL1.
– Gắn bó công ty (GB) gồm GB1, GB2, GB3.
Kết quả sau khi biểu diễn trên diagram SMARTPLS:
2.1 Chất lượng biến quan sát Outer Loading
Trong bài viết Phân tích mô hình ước lượng trên SMARTPLS chúng ta đã đề cập đến hệ số tải ngoài outer loading của các biến quan sát. Đây là chỉ số thể hiện mức độ liên kết giữa biến quan sát với biến tiềm ẩn mẹ.
Về bản chất, outer loading trong SMARTPLS chính là căn bậc hai trị tuyệt đối giá trị R2 phép hồi quy tuyến tính từ biến tiềm ẩn mẹ lên biến quan sát con. Ví dụ, biến tiềm ẩn A được đo bằng ba biến quan sát A1, A2, A3. Hệ số tải ngoài của biến quan sát A1 = 0.782 nghĩa là phép hồi quy từ A tác động lên A1 cho giá trị R2 = (0.782)2 = 0.612, biến tiềm ẩn A giải thích được 61.2% sự biến biên của biến quan sát A1.
Hair và cộng sự (2016) cho rằng hệ số tải ngoài outer loading cần lớn hơn hoặc bằng 0.708 biến quan sát đó là chất lượng. Bởi vì 0.7082 = 0.5, nghĩa là biến tiềm ẩn đã giải thích được 50% sự biến thiên của biến quan sát. Theo quan điểm của Hair và cộng sự, có thể thấy rằng các nhà nghiên cứu này đánh giá một biến quan sát con là chất lượng nếu biến tiềm ẩn mẹ giải thích được tối thiểu 50% sự thay đổi của biến quan sát đó. Để dễ dàng ghi nhớ hơn, các nhà nghiên cứu làm tròn thành ngưỡng 0.7 thay vì số lẻ 0.708. Trong ví dụ bên dưới, biến CV1, DK4 và TL4 có hệ số tải nhỏ hơn 0.7, cần xem xét loại bỏ khỏi mô hình.
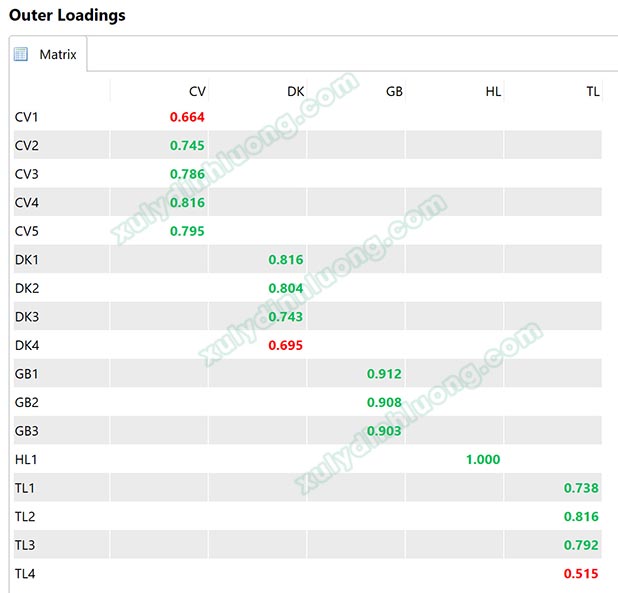
Mặc dù có nhiều quan điểm khác nhau được đưa ra khi đánh giá chất lượng biến quan sát qua chỉ số outer loading. Kết quả ở các nghiên cứu đó đưa ra những ngưỡng outer loading khác nhau, tuy nhiên, ngưỡng 0.7 là ngưỡng được dùng phổ biến nhất ở đại đa số các trường hợp. Một biến quan sát có outer loading dưới 0.7 nên được loại bỏ và phân tích lại mô hình.
Outer Loading ≥ 0.7 (Hair và cộng sự, 2016)
Để xem giá trị hệ số tải ngoài outer loading trên SMARTPLS, chúng ta chạy PLS Algorithm (xem cách chạy tại đây).

2.2 Độ tin cậy thang đo Reliability
Chúng ta đánh giá độ tin cậy thang đo trên SMARTPLS qua hai chỉ số chính là Cronbach’s Alpha và Composite Reliability. Độ tin cậy Cronbach Alpha chúng ta đã làm quen trên SPSS. Trong SMARTPLS chỉ số này được tính toán tương tự và ngưỡng chấp nhận cũng như trên SPSS. Các bạn xem ngưỡng đánh giá tại bài viết Phân tích độ tin cậy Cronbach’s Alpha trong SPSS.
Độ tin cậy tổng hợp Composite Reliability (CR) được nhiều nhà nghiên cứu ưu tiên lựa chọn hơn Cronbach’s Alpha bởi Cronbach’s Alpha đánh giá thấp độ tin cậy hơn so với CR. Chin (1998) cho rằng trong nghiên cứu khám phá, CR phải từ 0.6 trở lên. Với các nghiên cứu khẳng định, ngưỡng 0.7 là mức phù hợp của chỉ số CR (Henseler & Sarstedt, 2013). Nhiều nhà nghiên cứu khác cũng đồng ý mức 0.7 là ngưỡng đánh giá phù hợp cho đại đa số trường hợp như Hair và cộng sự (2010), Bagozzi & Yi (1988).
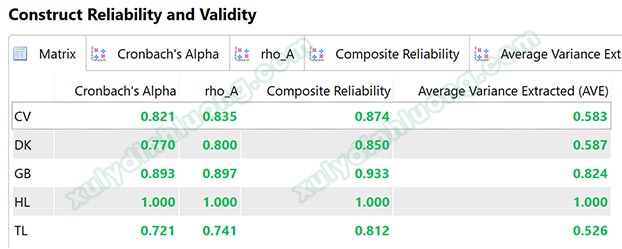
Nếu một thang đo không đạt ngưỡng độ tin cậy, cần loại lần lượt từng biến quan sát có outer loading thấp nhất để cải thiện độ tin cậy. Nếu đã loại hết biến không đủ điều kiện nhưng thang đo vẫn không đạt ngưỡng độ tin cậy, chúng ta sẽ kết luận thang đo không đảm bảo độ tin cậy và không sử dụng thang đo đó cho các phân tích định lượng phía sau.
Cronbach’s Alpha ≥ 0.7 (DeVellis, 2012)
Composite Reliability CR ≥ 0.7 (Bagozzi & Yi, 1988)
Để xem Cronbach’s Alpha và Composite Reliability trên SMARTPLS, chúng ta chạy PLS Algorithm (xem cách chạy tại đây).

2.3 Tính hội tụ Convergence
Để đánh giá tính hội tụ trên SMARTPLS, chúng ta sẽ dựa vào chỉ số phương sai trung bình được trích AVE (Average Variance Extracted). Hock & Ringle (2010) cho rằng một thang đo đạt giá trị hội tụ nếu AVE đạt từ 0.5 trở lên. Mức 0.5 (50%) này mang ý nghĩa biến tiềm ẩn mẹ trung bình sẽ giải thích được tối thiểu 50% biến thiên của từng biến quan sát con.
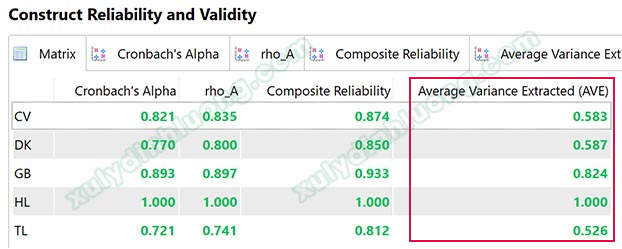
Một nhược điểm trong cách tính chỉ số AVE là đánh giá đồng đều các biến quan sát với nhau, không xem xét đến các biến quan sát có hệ số tải ngoài thấp. Trong đánh giá mô hình đo lường, một biến quan sát có hệ số tải ngoài thấp (ví dụ dưới 0.4) nhưng hệ số tải ngoài của các biến quan sát còn lại rất cao thì AVE vẫn đạt ngưỡng 0.5. Do đó, trước khi đánh giá AVE, chúng ta cần đánh giá chất lượng biến quan sát và kiểm tra độ tin cậy thang đo trước để loại bỏ các biến quan sát không có ý nghĩa.
Nếu một thang đo không đạt độ hội tụ, chúng ta cũng loại bỏ lần lượt từng biến quan sát có outer loading thấp nhất để cải thiện độ hội tụ. Nếu sau quá trình loại biến, tính hội tụ vẫn không đảm bảo, chúng ta kết luận thang đo không đảm bảo tính hội tụ và không sử dụng thang đo cho các phân tích định lượng phía sau.
Average Variance Extracted AVE ≥ 0.5 (Hock & Ringle, 2010)
Để xem AVE trên SMARTPLS, chúng ta chạy PLS Algorithm (xem cách chạy tại đây).

2.4 Tính phân biệt Discriminant
Giá trị phân biệt cho thấy tính khác biệt của một cấu trúc khi so sánh với các cấu trúc khác trong mô hình. Cách tiếp cận truyền thống để đánh giá tính phân biệt là sử dụng chỉ số căn bậc hai AVE do Fornell and Larcker (1981) đề xuất. Phương pháp truyền thống này có những thiếu sót và cần một phương pháp đánh giá chính xác hơn. Henseler và cộng sự (2015) đã sử dụng các nghiên cứu mô phỏng để chứng minh rằng giá trị phân biệt được đánh giá một cách tốt hơn bởi chỉ số HTMT mà họ đã phát triển. SMARTPLS sử dụng cả hai cách đánh giá tính phân biệt này, tuy nhiên vẫn chú trọng vào HTMT hơn.
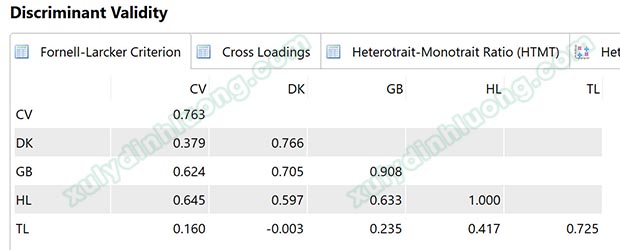
Fornell and Larcker (1981) khuyến nghị rằng tính phân biệt được đảm bảo khi căn bậc hai của AVE cho mỗi biến tiềm ẩn cao hơn tất cả tương quan giữa các biên tiềm ẩn với nhau. Cấu trúc trình bày bảng Fornell and Larcker như mẫu bên dưới ở tất cả các phần mềm SEM. Phần số ở đầu mỗi cột chính là giá trị căn bậc hai AVE (0.763, 0.766, 0.908, 1.000, 0.725), và phần số bên dưới là tương quan giữa các biến tiềm ẩn. Trong bảng này có một giá trị căn bậc hai AVE bằng 1 ở biến tiềm ẩn HL bởi biến này chỉ được đo bằng một biến quan sát HL1.
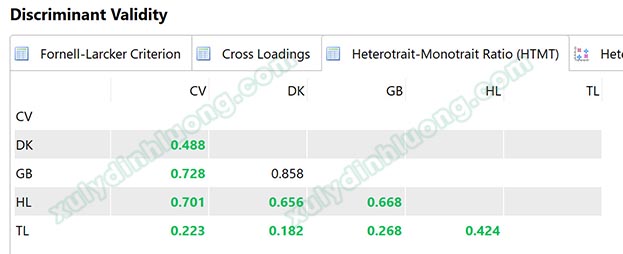
Với chỉ số HTMT, Garson (2016) cho rằng giá trị phân biệt giữa hai biến tiềm ẩn được đảm bảo khi chỉ số HTMT nhỏ hơn 1. Henseler và cộng sự (2015) đề xuất rằng nếu giá trị này dưới 0.9, giá trị phân biệt sẽ được đảm bảo. Trong khi đó, Clark & Watson (1995) và Kline (2015) sử dụng ngưỡng tiêu chuẩn nghiêm ngặt hơn là 0.85. SMARTPLS ưu tiên lựa chọn ngưỡng là 0.85 trong đánh giá.
Khi đánh giá HTMT, chúng ta NÊN thực hiện bootstrapping để xem giá trị này có khác 1 một cách có ý nghĩa thống kê hay không. Nếu lấy độ tin cậy của phép bootstrap bằng 95%, chúng ta sẽ xét đoạn phân vị 2.5% tới 97.5% có chứa giá trị 1 hay không. Nếu đoạn phân vị chứa giá trị 1, nghĩa là tính phân biệt không được đảm bảo, ngược lại, nếu đoạn phân vị không chứa giá trị 1 nghĩa là tính phân biệt được đảm bảo. Khắt khe hơn, chúng ta sẽ xét giá trị 0.9 hoặc 0.85 thay vì giá trị 1.
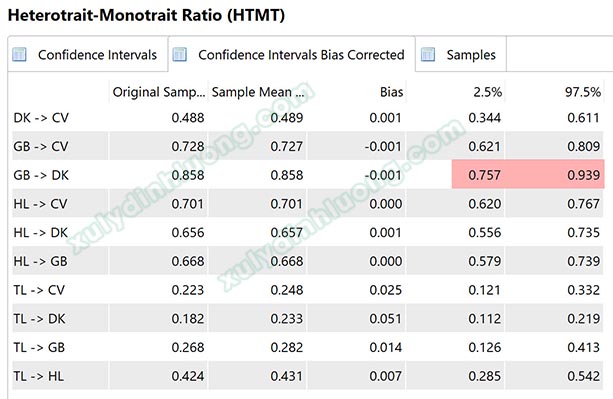
Khi đánh giá tính phân biệt, chúng ta sẽ cần lưu ý vai trò biến độc lập và phụ thuộc. Bởi khi biến độc lập tác động rất mạnh lên phụ thuộc, HTMT giữa biến độc lập với phụ thuộc có thể sẽ cao vượt ngưỡng 0.85. Lúc này giải pháp là không đánh giá HTMT giữa độc lập với phụ thuộc mà chỉ đánh giá giữa các biến độc lập với nhau. Trong ví dụ ở ảnh trên, DK (điều kiện làm việc) là một biến độc lập tác động lên GB (gắn bó với công ty), do điều kiện làm việc ảnh hưởng rất mạnh đến việc nhân viên có gắn bó với công ty hay không nên HTMT của cặp biến này bằng 0.858 > 0.85, đoạn phân vị [0.757;0.939] chứa giá trị 0.9.
Căn bậc hai AVE > Tương quan giữa các biến tiềm ẩn (Fornell and Larcker, 1981)
HTMT ≤ 0.85 (Kline, 2015)
Để xem bảng Fornell and Larcker và HTMT trên SMARTPLS, chúng ta chạy PLS Algorithm (xem cách chạy tại đây).

2.5 Độ phù hợp mô hình Model Fit
Như đã đề cập trong bài viết Kinh nghiệm trong lựa chọn giữa PLS-SEM và CB-SEM, thuật toán PLS không phù hợp cho việc đưa ra các chỉ số đánh giá độ phù hợp mô hình. Mặc dù SMARTPLS cung cấp một số chỉ số liên quan đến Model Fit, tuy nhiên, nhóm tác giả phát triển phần mềm và nhiều nhà nghiên cứu khác đã đưa cảnh báo về việc sử dụng các chỉ số này. Bạn có thể xem cảnh báo tại trang web chính thức của đội ngũ phát triển phần mềm SMARTPLS tại link này và link này.
Hair và cộng sự (2016) đã nhấn mạnh PLS-SEM tập trung vào khả năng dự báo thay vì khẳng định mô hình, do đó thuật toán PLS-SEM không phù hợp cho việc đánh giá mức độ phù hợp tổng thể của mô hình.
Không xét Model Fit trong SMARTPLS (Hair và cộng sự, 2016)
Xem thêm: Chạy Bootstrap và đánh giá mô hình cấu trúc trên SMARTPS
TÓM LẠI:
Khi đánh giá mô hình đo lường trên SMARTPLS, chúng ta sẽ quan tâm đến:
– Outer Loadings ≥ 0.7
– Cronbach’s Alpha ≥ 0.7
– Composite Reliability ≥ 0.7
– AVE ≥ 0.5
– HTMT ≤ 0.85
Nếu bạn gặp những vấn đề trong phân tích SMARTPLS, bạn có thể tham khảo dịch vụ SMARTPLS của Xử Lý Định Lượng ở đây hoặc liên hệ trực tiếp email xulydinhluong@gmail.com.











