Đánh giá tính hội tụ và tính phân biệt là một bước quan trọng trong phân tích mô hình đo lường trên SMARTPLS. Việc này nhằm đánh giá chất lượng của các nhân tố cũng như biến quan sát thành phần của các nhân tố trong mô hình.
1. Tính hội tụ trong SMARTPLS 3
Để đánh giá tính hội tụ trên SMARTPLS, chúng ta sẽ dựa vào chỉ số AVE (Average Variance Extracted – phương sai trung bình được trích). AVE đo lường mức độ mà một biến ẩn giải thích phương sai của các biến quan sát (chỉ báo) tương ứng. AVE được tính bằng cách tổng các giá trị của bình phương hệ số tải ngoài (outer loading) của tất cả các chỉ báo liên quan đến biến ẩn đó, chia cho tổng của bình phương hệ số tải trọng và các sai số (error) của nhân tố đó.
Hock & Ringle (2010) cho rằng một thang đo đạt giá trị hội tụ nếu AVE đạt từ 0.5 trở lên. Mức 0.5 (50%) này mang ý nghĩa nhân tố mẹ trung bình sẽ giải thích được tối thiểu 50% biến thiên của từng biến quan sát con. Hệ số AVE càng cao cho thấy sự hội tụ càng cao, ngược lại AVE càng thấp cho thấy sự hội tụ thang đo càng thấp.
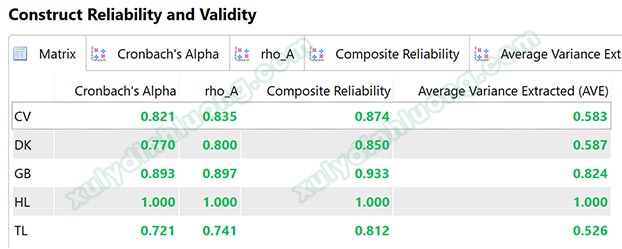
Nếu một thang đo không đạt ngưỡng AVE, chúng ta cũng loại bỏ lần lượt từng biến quan sát có outer loading thấp nhất để cải thiện chỉ số này. Nếu sau quá trình loại biến, tính AVE vẫn không tăng lên ngưỡng yêu cầu, chúng ta kết luận thang đo không đảm bảo tính hội tụ và không sử dụng thang đo cho các phân tích định lượng phía sau.
Để xem AVE trên SMARTPLS, chúng ta chạy PLS Algorithm (xem cách chạy tại đây).

2. Tính phân biệt trong SMARTPLS 3
2.1 Đánh giá tính phân biệt bằng bảng Fornell and Larcker
Fornell and Larcker (1981) khuyến nghị rằng tính phân biệt được đảm bảo khi căn bậc hai của AVE cho mỗi biến tiềm ẩn cao hơn tất cả tương quan giữa các biến tiềm ẩn với nhau. Xem chi tiết tại bài viết Đánh giá tính phân biệt thang đo bằng bảng Fornell and Larcker.
Căn bậc hai AVE > Tương quan giữa các biến tiềm ẩn (Fornell and Larcker, 1981)
Cấu trúc trình bày bảng Fornell and Larcker như mẫu bên dưới ở tất cả các phần mềm SEM. Phần số ở đầu mỗi cột chính là giá trị căn bậc hai AVE (0.763, 0.766, 0.908, 1.000, 0.725), và phần số bên dưới là tương quan giữa các biến tiềm ẩn. Trong bảng này có một giá trị căn bậc hai AVE bằng 1 ở biến tiềm ẩn HL bởi biến này chỉ được đo bằng một biến quan sát HL1.
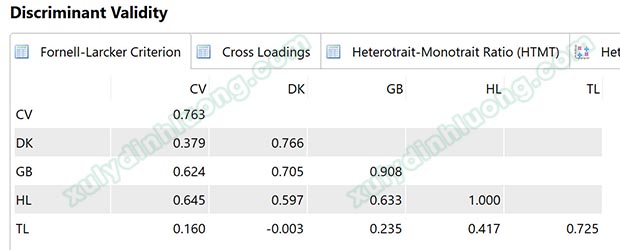
→ Căn bậc hai của AVE của từng biến tiềm ẩn lớn hơn các tương quan giữa các biến tiềm ẩn với nhau, do vậy tính phân biệt được đảm bảo.
2.2 Đánh giá tính phân biệt bằng bảng HTMT
Chỉ số HTMT được sử dụng để đo lường mức độ tách biệt giữa các biến ẩn trong mô hình và đo lường tính hợp lý của mô hình. HTMT được tính bằng cách lấy giá trị trung bình của tỷ lệ tương quan giữa các biến khác loại (heterotrait) và các biến cùng loại (monotrait), chia cho giá trị tối đa của tỷ lệ tương quan giữa các biến cùng loại.
Với chỉ số HTMT, Garson (2016) cho rằng giá trị phân biệt giữa hai biến tiềm ẩn được đảm bảo khi chỉ số HTMT nhỏ hơn 1. Henseler và cộng sự (2015) đề xuất rằng nếu giá trị này dưới 0.9, giá trị phân biệt sẽ được đảm bảo. Trong khi đó, Clark & Watson (1995) và Kline (2015) sử dụng ngưỡng tiêu chuẩn nghiêm ngặt hơn là 0.85. Ngưỡng 0.9 được sử dụng phổ biến nhất.
Khi giá trị của chỉ số HTMT cho một cặp biến ẩn là thấp, tức là giá trị của chỉ số HTMT nhỏ hơn hoặc bằng 0.9, thì ta có thể kết luận rằng tính phân biệt giữa các biến ẩn trong mô hình là tốt. Nếu giá trị của chỉ số HTMT cho một cặp biến ẩn là cao hơn 0.9, thì ta cần kiểm tra lại mô hình để xem có cần thực hiện các điều chỉnh để cải thiện tính phân biệt giữa các biến ẩn.
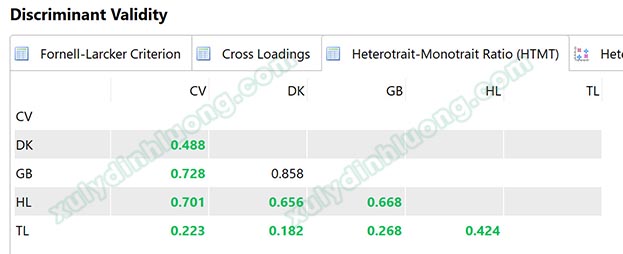
HTMT ≤ 0.9 (Hair và cộng sự, 2014)
Để xem bảng Fornell and Larcker và HTMT trên SMARTPLS, chúng ta chạy PLS Algorithm (xem cách chạy tại đây).













