Trong bài viết Phân tích mô hình ước lượng trên SMARTPLS chúng ta đã làm quen với cách thiết lập và phân tích mô hình ước lượng. Từ kết quả phân tích mô hình ước lượng, chúng ta đánh giá mô hình đo lường qua các yếu tố như chất lượng biến quan sát, độ tin cậy, tính hội tụ/phân biệt.
Bước tiếp theo, chúng ta sẽ phân tích bootstrap để đánh giá mô hình cấu trúc trên SMARTPLS 3. Kết quả có được từ bootstrap sẽ giúp người nghiên cứu kết luận được giả thuyết các mối quan hệ tác động trong mô hình.
Bài viết này sử dụng tập dữ liệu và cấu trúc biến đã được giới thiệu tại bài viết Cách nhập dữ liệu và vẽ mô hình đường dẫn trên SMARTPLS. Bạn nên mở xem lại bài viết để hiểu phần phân tích bên dưới.
1. Phân tích Bootstrap trên SMARTPLS 3
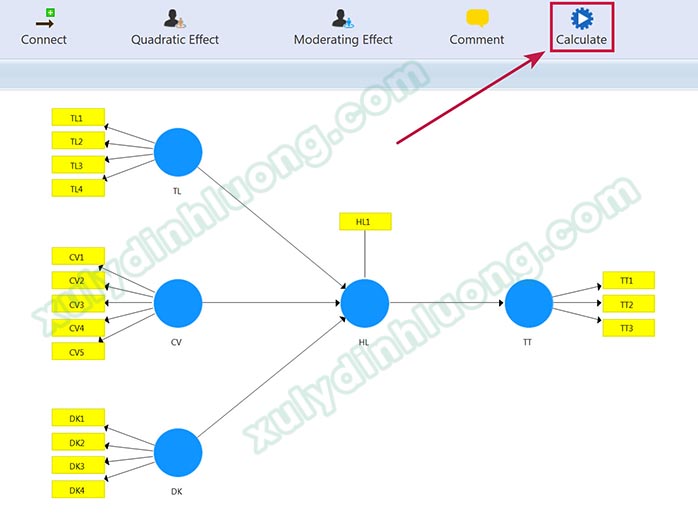
Cửa sổ Bootstrapping xuất hiện, tiến hành thiết lập phân tích bootstrap SMARTPLS 3 như sau:
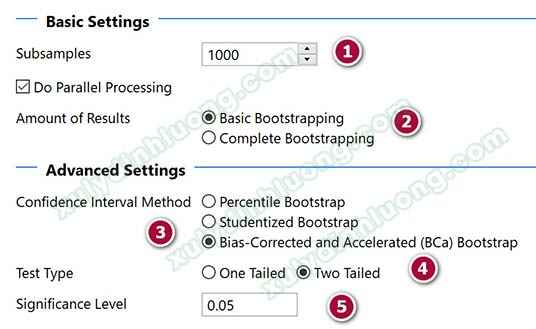
– Subsamples: Số lần bootstrap, thường chúng ta sẽ dùng 1000 hoặc 5000.
– Basic Bootstrapping/Complete Bootstrapping: Mặc định Bootstrap trên SMARTPL sẽ dùng Basic. Kết quả Basic sẽ xuất cho chúng ta kết quả bootstrap gồm Path Coefficients, Indirect Effects, Total Effects, Outer Loadings, and Outer Weights. Trường hợp chúng muốn xuất đầy đủ toàn bộ chỉ số, chúng ta sẽ chọn vào Complete Bootstrapping, tuy nhiên sẽ mất rất nhiều thời gian và yêu cầu máy tính hoạt động nặng. Do đó, nếu không cần thiết thì chúng ta chỉ cần dùng Basic là đủ.
– Confidence Interval Method: Chúng ta sẽ để mặc định Bias-Corrected and Accelerated (BCa), đây là lựa chọn tối ưu nhất. Chi tiết về 3 phương pháp, các bạn có thể tìm kiếm trên wikipedia về bootstrap.
– Test Type: Chọn Two Tailed để kiểm định hai đầu.
– Significance Level: Mức ý nghĩa của phép kiểm định, mặc định sẽ là 0.05 (5%), chúng ta có thể tùy chỉnh mức 10% hay 1% tùy tính chất nghiên cứu.
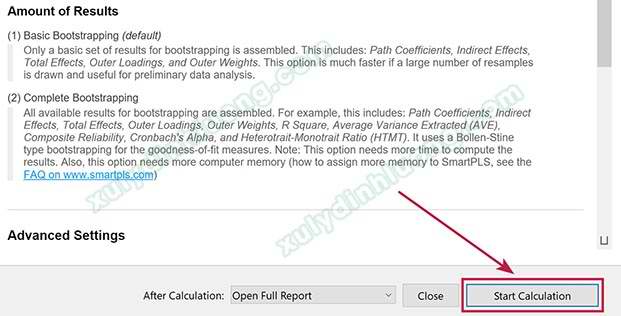
Tiếp tục nhấp vào Start Calculation để tiến hành phân tích bootstrap trên SMARTPLS.
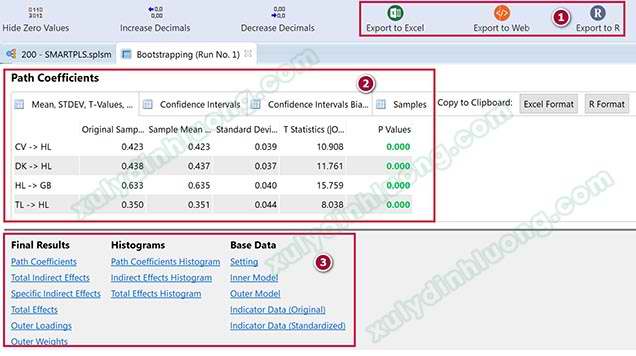
Output kết quả Bootstrap xuất hiện, chúng ta sẽ quan tâm đến 3 mục như ảnh bên dưới. Mục số 1, Export to Excel, Web, R để chúng ta xuất kết quả output ra file excel, file html hoặc định dạng của phần mềm R. Mục số 2 là giao diện hiển thị kết quả khi chúng ta nhấp vào các đầu mục kết quả ở mục 3. Mục số 3 là danh sách các kết quả phân tích bootstrap.
2. Đánh giá mô hình cấu trúc SEM trên SMARTPLS 3
2.1 Hiện thông số đường dẫn ở diagram
Chúng ta có thể cho hiển thị thông số kết quả các đường dẫn của mô hình SEM trên diagram để đánh giá trực quan và nhanh chóng kết quả đường dẫn.
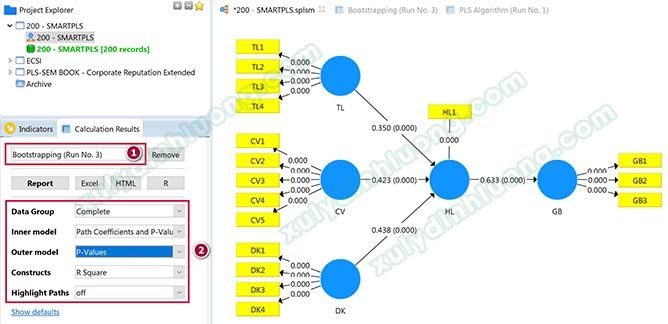
Trong mục số 1, chúng ta chọn vào loại kết quả cần hiển thị, cụ thể trong trường hợp này là Bootstrapping (Run No. 3). Khi chúng ta chạy nhiều lần bootstrapping, ở đây sẽ xuất hiện danh sách tất cả các lần chạy. Bạn muốn hiển thị kết quả lần chạy nào, sẽ chọn tương ứng lần chạy đó.
Với mục số 2, chúng ta sẽ tùy chọn ở 2 mục Inner model và Outer model các thông số hiển thị:
- Inner model: kết quả đường dẫn giữa các biến tiềm ẩn (mối quan hệ các biến tròn màu xanh). Tại đây có 4 lựa chọn:
- P-Values: giá trị sig mối quan hệ tác động ở đường dẫn đó.
- Path Coefficients and P-Values: hệ số tác động và giá trị sig.
- Path Coefficients and T-Values: hệ số tác động và giá trị kiểm định t.
- T-Values: giá trị kiểm định t.
- Thường chúng ta sẽ cho hiển thị Path Coefficients and P-Values để vừa hiển thị hệ số tác động, vừa hiển thị kết quả mối tác động đó là có ý nghĩa hay không có ý nghĩa.
- Outer model: kết quả đường dẫn giữa biến tiềm ẩn với các biến quan sát (mối quan hệ giữa biến tròn xanh và các biến hình chữ nhật vàng tương ứng). Tại đây có 4 lựa chọn:
- Outer Weights/Loadings and P-Values: hệ số tải của biến quan sát và giá trị sig.
- Outer Weights/Loadings and T-Values: hệ số tải của biến quan sát và giá trị kiểm định t.
- P-Values: giá trị sig mối quan hệ tác động ở đường dẫn đó.
- T-Values: giá trị kiểm định t.
- Thường chúng ta sẽ cho hiển thị P-Values để biết được biến quan sát có ý nghĩa hay không. Hoặc chúng ta có thể cho hiển thị Outer Weights/Loadings and P-Values cũng được, nhưng mô hình nhìn sẽ chật chội và hơi rối.
Sau khi đã cho hiển thị các thông số mong muốn, chúng ta sẽ dùng công cụ chụp ảnh màn hình máy tính để chụp diagram này và dán vào phần trình bày đánh giá mô hình cấu trúc SMARTPLS của bài luận.
2.2 Đánh giá cộng tuyến/đa cộng tuyến
Để đánh giá đa cộng tuyến, chúng ta sẽ sử dụng kết quả của phân tích PLS Algorithm. Cách chạy phân tích PLS Algorithm bạn xem tại đây.
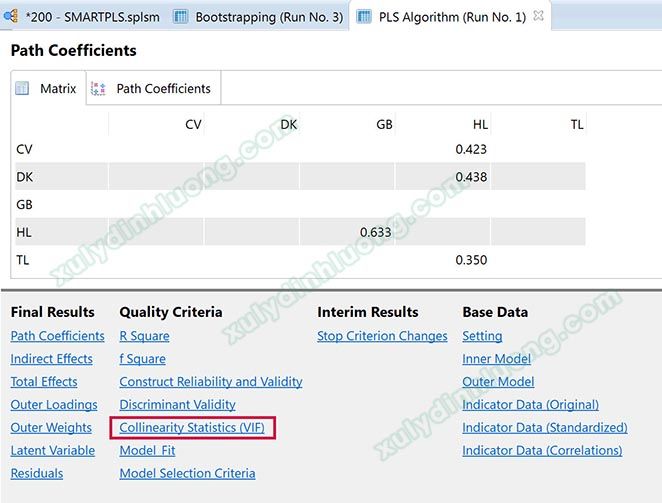
Nhấp vào Collinearity Statistics (VIF) để xem kết quả VIF. Kết quả VIF được chia làm hai vùng: Outer VIF và Inner VIF.
- Inner VIF Values: Đánh giá hiện tượng đa cộng tuyến giữa các biến tiềm ẩn. Đây là mục quan trọng nhất, bởi đa cộng tuyến giữa các biến tiềm ẩn độc lập là vấn đề nghiêm trọng.
- Outer VIF Values: Đánh giá hiện tượng đa cộng tuyến giữa các biến quan sát. Với các cấu trúc được xây dựng theo mô hình reflective, chúng ta không cần quan tâm đến chỉ số này. Với các cấu trúc được xây dựng theo mô hình formative, chỉ số này cao cũng nghiêm trọng như Inner VIF Values, chúng ta cần phải xử lý. Xem thêm bài viết Lý thuyết mô hình đo lường Formative, Reflective.

Cách bố trí bảng VIF ở dạng ma trận. Phần hàng màu đỏ biểu thị cho biến phụ thuộc, phần cột màu vàng biểu thị cho biến độc lập. Phần phụ thuộc chúng ta chỉ thấy 2 biến có kết quả là GB và HL bởi trong mô hình SEM đang đánh giá, chỉ có 2 biến này là phụ thuộc và cần xét đa cộng tuyến giữa các biến độc lập tác động lên mỗi biến phụ thuộc này.
- Biến phụ thuộc HL: có 3 biến độc lập tác động lên nó gồm CV, DK và TL nên cột HL có 3 giá trị.
- Biến phụ thuộc GB: có 1 biến độc lập tác động lên nó là HL nên cột GB có 1 giá trị.
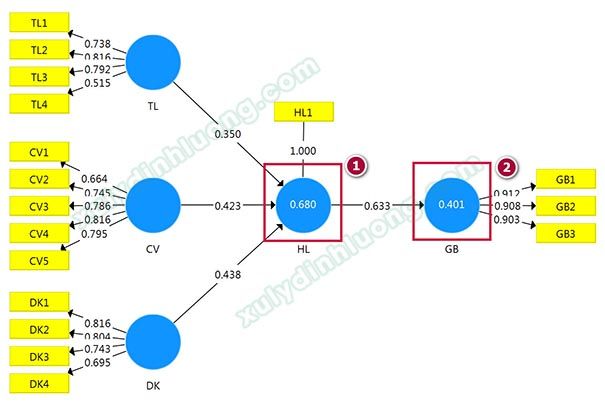
Theo Hair và cộng sự (2019), nếu VIF từ 5 trở đi, mô hình có khả năng rất cao xuất hiện hiện tượng đa cộng tuyến. Ngưỡng đánh giá VIF do nhóm tác giả đề xuất như sau:
- VIF ≥ 5: Khả năng xuất hiện đa cộng tuyến là rất cao.
- 3 ≤ VIF ≤ 5: Có thể gặp hiện tượng đa cộng tuyến.
- VIF < 3: Có thể không có hiện tượng đa cộng tuyến.
Các cấu trúc trong mô hình SEM ở trên đều là reflective, hệ số VIF kết quả đều nhỏ hơn 3, do vậy không xảy ra đa cộng tuyến trong mô hình.
2.3 Đánh giá các mối quan hệ tác động
Để đánh giá các mối quan hệ tác động, chúng ta sẽ sử dụng kết quả của phân tích Bootstrap.
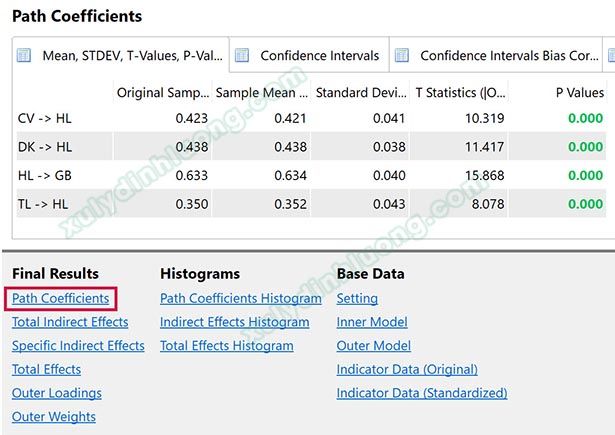
Nhấp vào Path Coefficients để xem kết quả. Chúng ta sẽ quan tâm chủ yếu vào hai cột (1) Original Sample (hệ số tác động chuẩn hóa) và (2) P Values (giá trị sig so sánh với mức ý nghĩa 0.05).
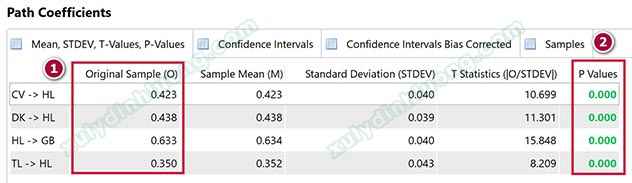
Kết quả ở trên cho thấy toàn bộ P Values của các mối tác động đều bằng 0.000 < 0.05, do vậy các mối tác động này đều có ý nghĩa thống kê. Có 3 biến tác động lên HL là CV, DK và TL. Hệ số tác động chuẩn hóa của 3 biến này lần lượt là 0.423, 0.438, 0.350. Như vậy, mức độ tác động của 3 biến này lên HL theo thứ tự từ mạnh đến yếu là DK, CV, TL.
2.4 Mức độ giải thích của biến độc lập cho phụ thuộc (R bình phương)
Để đánh giá hệ số R bình phương, chúng ta sẽ sử dụng kết quả của phân tích PLS Algorithm.
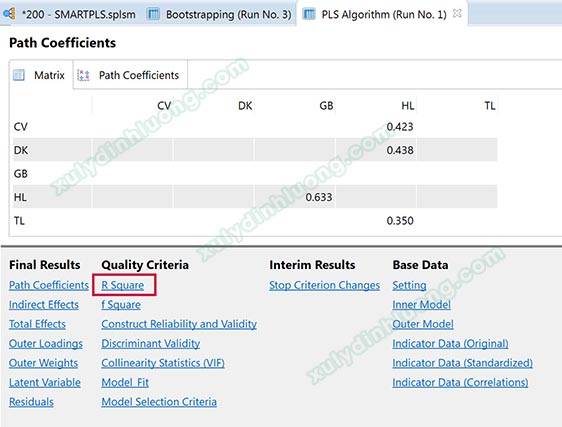
Trong SMARTPLS, chúng ta có hai kết quả là R bình phương (R Square) và R bình phương hiệu chỉnh (R Square Adjusted).
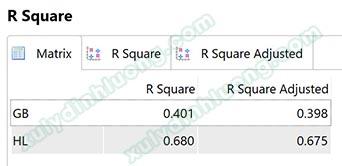
Ý nghĩa chỉ số này hoàn toàn tương tự như ở hồi quy tuyến tính trên SPSS, các bạn xem tại bài viết Ý nghĩa của giá trị R bình phương hiệu chỉnh trong hồi quy. Nếu các kết quả phân tích có cả hai chỉ số này, chúng ta sẽ ưu tiên sử dụng chỉ số R bình phương hiệu chỉnh.
Trường hợp cụ thể ở ví dụ bên trên, R bình phương hiệu chỉnh của HL bằng 0.675, như vậy các biến độc lập đã giải thích được 67.5% sự biến thiên (phương sai) của biến HL, còn lại 32.5% là từ sai số hệ thống và từ các yếu tố khác nằm ngoài mô hình.
Giá trị R bình phương (R bình phương hiệu chỉnh cũng tương tự) nằm trong khoảng từ 0 đến 1, càng tiến gần về 1 cho thấy các biến độc lập giải thích cho biến phụ thuộc càng nhiều. Rất khó khăn để đưa ra quy tắc kinh nghiệm chấp nhận giá trị R bình phương, điều này phụ thuộc vào sự phức tạp của mô hình và lĩnh vực nghiên cứu.
2.5 Giá trị effect size (f bình phương)
Để đánh giá hệ số effect size f2 (f bình phương hoặc f square) , chúng ta sẽ sử dụng kết quả của phân tích PLS Algorithm.
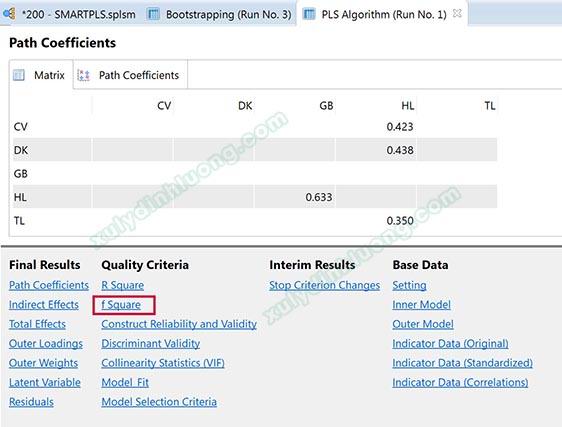
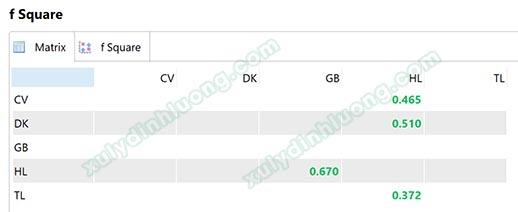
Cách trình bày bảng f bình phương (f Square) tương tự như bảng Inner VIF Values. Hệ số f bình phương cho biết mức độ ảnh hưởng của biến độc lập lên biến phụ thuộc là mạnh hay yếu.
Trong nhiều tình huống thứ tự độ lớn của hệ số tác động chuẩn hóa (cột Original sample trong bảng Path coefficients) trùng với thứ tự mạnh yếu của hệ số f square nên cả hai chỉ số đều có thể dùng để so sánh sự tác động mạnh yếu của các biến độc lập khi chúng cùng tác động lên một biến phụ thuộc. Tuy nhiên, không phải lúc nào thứ tự f square cũng giống thứ tự độ lớn hệ số hồi quy chuẩn hóa. Chi tiết so sánh giữa effect size f square và hệ số đường dẫn, bạn xem tại bài viết này.
– Muốn so sánh biến độc lập nào tác động mạnh hơn lên cùng một biến phụ thuộc, chúng ta sẽ dùng hệ số tác động chuẩn hóa.
– Muốn xem mức độ tác động của các biến độc lập lên biến phụ thuộc là mạnh, trung bình hay yếu chúng ta sẽ dùng hệ số f square.
Cohen (1988) đã đề xuất bảng chỉ số f Square để đánh giá tầm quan trọng của các biến độc lập như sau:
- f Square < 0.02: mức tác động là cực kỳ nhỏ hoặc không có tác động.
- 0.02 ≤ f Square < 0.15: mức tác động nhỏ.
- 0.15 ≤ f Square < 0.35: mức tác động trung bình.
- f Square ≥ 0.35: mức tác động lớn.
Trong ví dụ cụ thể bên trên, tất cả f Square đều trên 0.35, như vậy các biến độc lập trong mô hình SEM đều có ảnh hưởng lớn lên biến phụ thuộc.
TÓM LẠI:
Khi đánh giá mô hình cấu trúc trên SMARTPLS, chúng ta sẽ quan tâm đến:
– Hệ số VIF đánh giá đa cộng tuyến
– Hệ số tác động và ý nghĩa các mức động của đường dẫn
– Hệ số R bình phương
– Hệ số f bình phương
Xem thêm: Xử lý biến điều tiết moderator trên SMARTPLS 3
Nếu bạn gặp những vấn đề trong phân tích SMARTPLS, bạn có thể tham khảo dịch vụ SMARTPLS của Xử Lý Định Lượng ở đây hoặc liên hệ trực tiếp email xulydinhluong@gmail.com.












