Loại bỏ điểm dị biệt bằng Scatter Plot và Casewise Diagnostics hồi quy

Bên cạnh việc loại bỏ điểm dị biệt bằng Boxplot, chúng ta có thể sử dụng đến đồ thị Scatter phần dư chuẩn hóa và bảng Casewise Diagnostics từ hồi quy để cải thiện kết quả hồi quy tuyến tính bội.

1. Xử lý điểm dị biệt bằng Scatter Plot

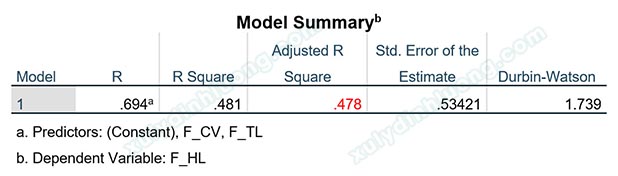
Thực hành với tập dữ liệu mẫu (xem thông tin cuối bài viết), chúng ta có ba biến F_TL, F_CV và F_HL là biến đại diện được tạo từ các biến quan sát. F_HL là biến phụ thuộc, trong khi đó F_TL và F_CV là hai biến độc lập. Thực hiện hồi quy tuyến tính bội theo hướng dẫn ở chương HỒI QUY TUYẾN TÍNH LINEAR REGRESSION, chúng ta có được giá trị Adjusted R Square trong bảng Model Summary bằng 0.478. Đây là một chỉ số thể hiện mức độ phù hợp của mô hình hồi quy, chỉ số này càng tiến về 1, càng cho thấy mô hình hồi quy là phù hợp.

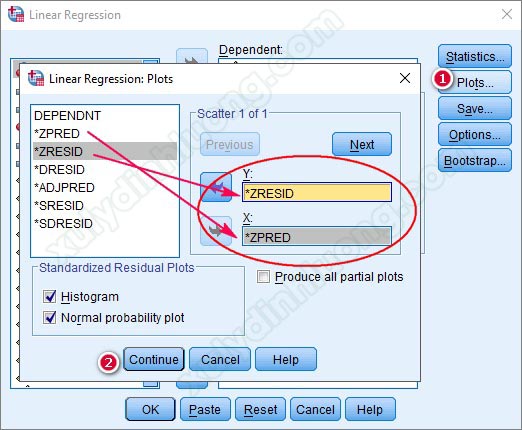
Để xuất hiện được đồ thị Scatter, khi thực hiện phân tích hồi quy tuyến tính bội, các bạn vào mục Plots, tích chọn kéo biến ZRESID thả vào ô Y, kéo biến ZPRED thả vảo ô X như hình bên dưới. 

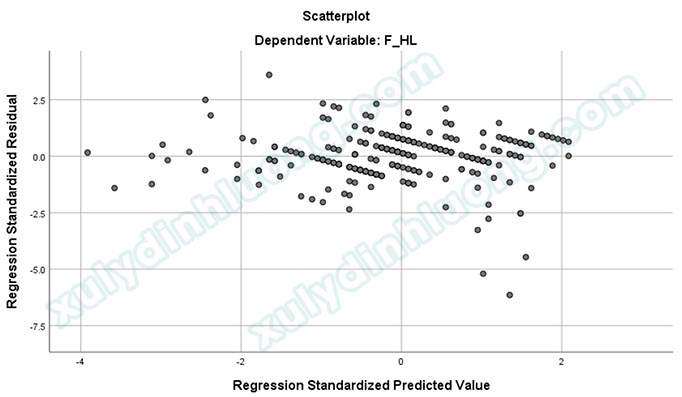
Các bạn nên phân tích hồi quy chính xác theo hướng tại bài viết Phân tích và đọc kết quả hồi quy tuyến tính bội trên SPSS để xuất ra đầy đủ các bảng, đồ thị cần dùng cho nhận xét kết quả, bao gồm cả đồ thị Scatter.

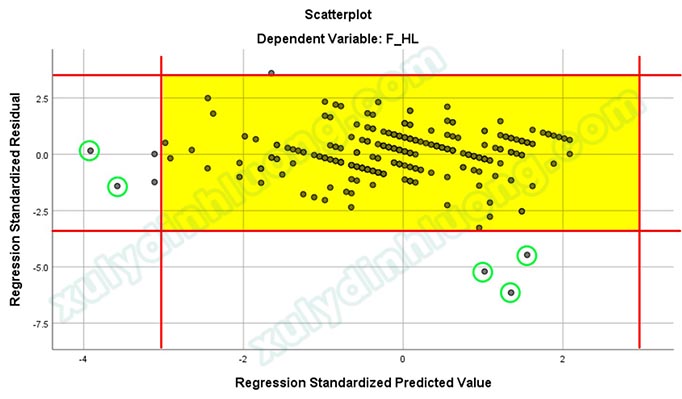
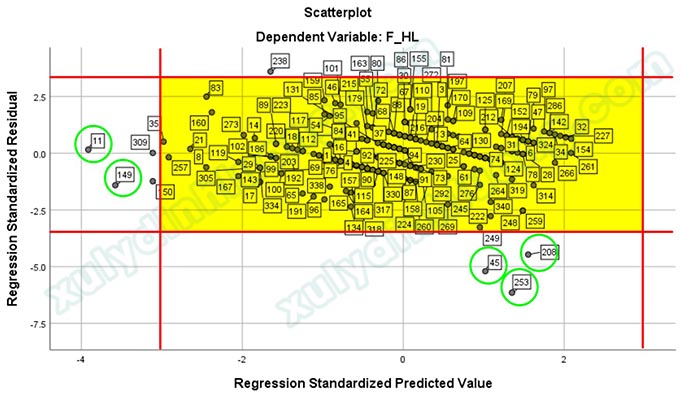
Theo quy luật Empirical hay còn gọi là quy luật 68-95-99.7 trong phân phối chuẩn, các điểm dữ liệu nằm ngoài vùng -3 đến 3 ở cả hai trục hoành và trục tung sẽ là các điểm dị biệt (phần giải thích sẽ được trình bày ở mục kế tiếp). Nếu kết quả hồi quy không tốt, chúng ta nên xem xét loại bỏ các điểm này để cải thiện mô hình. Có năm điểm đánh dấu bằng màu xanh lá nằm ngoài khu vực tô vàng chính là các điểm dị biệt.

Chúng ta sẽ yêu cầu phần mềm hiện tên quan sát của điểm dữ liệu để xác định ID của năm điểm dị biệt trên bằng cách nhấp đôi chuột vào đồ thị, chọn vào biểu tượng khoanh tròn như ảnh bên dưới, sau đó nhấp vào nút Close để đóng cửa sổ.

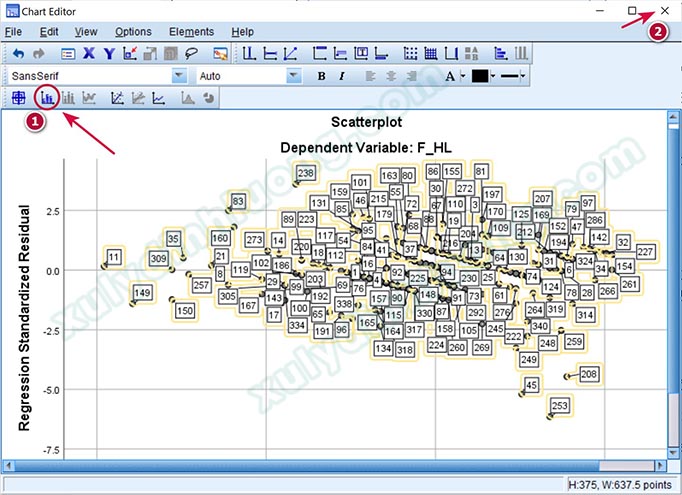
Như vậy, năm điểm dị biệt được xác định là các quan sát: 11, 149, 45, 208, 253.

Dùng Select Cases để yêu cầu phần mềm không tính toán các quan sát này. Trong hộp thoại Select Cases: If, chúng ta sử dụng hàm: ID ~= 11 AND ID ~= 149 AND ID ~= 45 AND ID ~= 208 AND ID ~= 253. Thực hiện hồi quy tuyến tính bội với tập dữ liệu đã được loại bỏ các quan sát dị biệt để xem xét sự thay đổi.

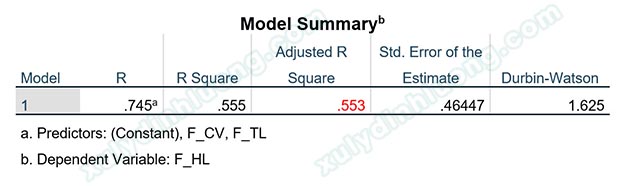
Giá trị Adjusted R Square mới bằng 0.553, lớn hơn rất nhiều so với giá trị ban đầu 0.478, độ phù hợp mô hình hồi quy đã cải thiện rất đáng kể. Đánh đổi sự cải thiện này, chúng ta loại đi 5 quan sát dị biệt. Số lượng 5 quan sát so với cỡ mẫu 350 là rất nhỏ, do vậy, chúng ta nên loại bỏ các quan sát dị biệt này để có được kết quả hồi quy tốt hơn.

 Xem thêm: Loại bỏ điểm dị biệt outliers bằng đồ thị Boxplot

 Xem thêm: Điểm dị biệt outliers và quy luật Empirical

2. Xử lý điểm dị biệt bằng Casewise Diagnostics

Khi thực hiện phân tích hồi quy tuyến tính, SPSS có chức năng nhận diện tự động điểm dị biệt. Để làm được điều này, trong tùy chọn Statistics, chúng ta tích vào mục Casewise diagnostics và nhập giá trị 2 hoặc 3 standard deviation (độ lệch chuẩn) vào ô Outliers outside. Thường chúng ta sẽ xét điểm dị biệt ngoài vùng 3 độ lệch chuẩn trước, nếu xử lý xong các điểm dị biệt này nhưng kết quả vẫn không khả quan, chúng ta mới xét điểm dị biệt ngoài vùng 2 độ lệch chuẩn.

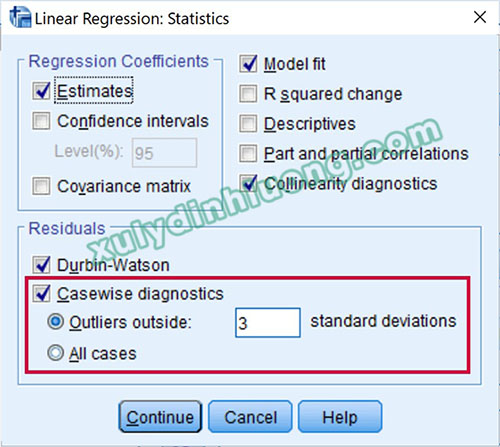
Tiếp tục thực hành phân tích hồi quy trên tập dữ liệu mẫu với ba biến F_TL, F_CV và F_HL. Tại Casewise diagnostics nhập giá trị 3 để phát hiện điểm dị biệt nằm ngoài vùng 3 độ lệch chuẩn. Kết quả hồi quy cho chúng ta giá trị Adjusted R Square bằng 0.478 và bảng Casewise Diagnostics chứa các quan sát dị biệt gồm: 45, 208, 238, 249, 253.

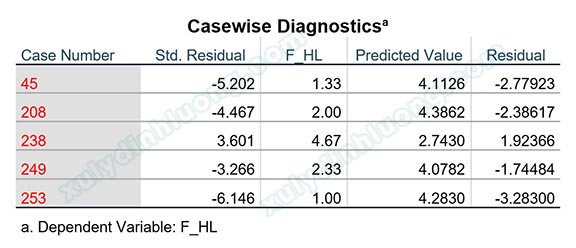
Dùng Select Cases để yêu cầu phần mềm không tính toán các quan sát này. Trong hộp thoại Select Cases: If, chúng ta sử dụng hàm: ID ~= 45 AND ID ~= 208 AND ID ~= 238 AND ID ~= 249 AND ID ~= 253. Thực hiện hồi quy tuyến tính bội với tập dữ liệu đã được loại bỏ các quan sát dị biệt để xem xét sự thay đổi.

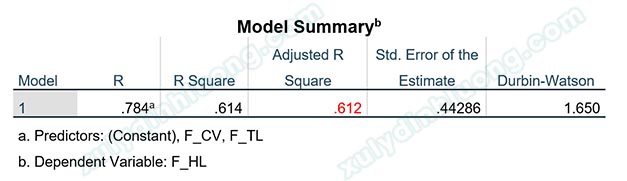
Giá trị Adjusted R Square mới bằng 0.612 > 0.478. Có thể thấy độ phù hợp của mô hình đã tốt hơn rất nhiều sau khi loại bỏ 5 quan sát dị biệt.